高校数学[総目次]
数学Ⅱ 第1章 式と証明
| スライド | ノート | |
| 1. 整式の除法 | [無料] | |
| 2. 分数式 | [無料] | |
| 3. 恒等式 | [無料] | |
| 4. 等式の証明 | [無料] | |
| 5. 不等式の証明 | [無料] |
5. 不等式の証明
5.1 不等式の証明
$A>B$ の証明の仕方
① $A-B=\cdots >0$ を示す．
② 有名不等式の利用．
例題1 $a\!>\!b,\ c\!>\!d$ のとき，$a\!+\!c\!>\!b\!+\!d$ を示せ．
$a>b,c>d$ より $a-b>0$，$c-d>0$．
よって証明すべき不等式 $a+c>b+d$ について，
\[\begin{align*}
(\mbox{左辺})-(\mbox{右辺})&=(a+c)-(b+d)\\[5pt]
&=(a-b)+(c-d)\\[5pt]
&>0+0\\[5pt]
&=0
\end{align*}\]
■
例題2 不等式 $|a\!+\!b|\!\leqq\!|a|\!+\!|b|$ を示せ．
確認 $a\geqq0$，$b\geqq0$ のとき， \[a\geqq b\iff a^2\geqq b^2\]
\[\begin{align*} (\mbox{右辺})^2-(\mbox{左辺})^2&=(|a|+|b|)^2-|a+b|^2\\[5pt] &=(|a|^2+2|a||b|+|b|^2)-(a^2+2ab+b^2)\\[5pt] &=(a^2+2|a||b|+b^2)-(a^2+2ab+b^2)\\[5pt] &=2(|a||b|-ab)\\[5pt] &\geqq 0 \end{align*}\] \[\therefore (\mbox{左辺})^2\leqq(\mbox{右辺})^2\] 左辺，右辺共に非負の数であるから， \[(\mbox{左辺})\leqq(\mbox{右辺})\] 等号成立は，$a$ と $b$ が共に0以上，または共に0以下のとき．
■
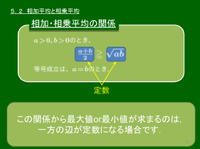
5.2 相加平均と相乗平均
相加・相乗平均の関係式 $a>0,b>0$ のとき，\[\frac{a+b}2\geqq\sqrt{ab}\] 等号成立は，$a=b$ のとき．
証明
$a>0,b>0$ であるから， \[\begin{align*} &\sqrt{ab}=\sqrt a\sqrt b\\[5pt] & a=(\sqrt a)^2\\[5pt] &b=(\sqrt b)^2 \end{align*}\] が成り立つことに注意して， \[\begin{align*} (\mbox{左辺})-(\mbox{右辺})&=\frac{a+b}2-\sqrt{ab}\\[5pt] &=\frac{a+b-2\sqrt{ab}}2\\[5pt] &=\frac{(\sqrt a)^2-2\sqrt a\sqrt b+(\sqrt b)^2}2\\[5pt] &=\frac{(\sqrt a-\sqrt b)^2}2\ \ \cdots\mbox{①}\\[5pt] &\geqq 0 \end{align*}\] 等号成立，即ち (左辺)$-$(右辺)$=0$ となるのは，①の分子が0となるときで，$a>0,b>0$ により \[\sqrt a-\sqrt b=0\iff \sqrt a=\sqrt b\iff a=b\] となるから $a=b$ のときである．
■
補足
① $\dfrac{a+b}2$，$\sqrt{ab}$ をそれぞれ $a$ と $b$ の相加平均，相乗平均という．
② しばしば分母の2を払った \[x+y\geqq2\sqrt{xy}\] の形で用いられる．
注意
相加・相乗平均の関係式を用いる際は，「$a>0, b>0$」の確認を必ず行う．
例題 $x\!>\!0$ のとき，不等式 $x\!+\!\dfrac1x\!\geqq\! 2$ を示せ．
$x>0,\ \dfrac1x>0$ であるから，相加・相乗平均の関係により， \[x+\frac 1x\geqq2\sqrt{x\cdot\frac1x}=2\] 等号成立は， \[\begin{align*} x=\frac1x&\iff x^2=1\ \ (\because x>0)\\[5pt] &\iff x=1\ \ (\because x>0) \end{align*}\] により，$x=1$ のとき．
■
発展的注意
相加・相乗平均の関係の良さは，評価精度の高さ，即ち等号が成立するケースがある，という点にある．($x^2\geqq -1$ と評価したところで，$x^2=-1$ となる実数 $x$ はない．)
この評価の正確さから，しばしば関数の最大・最小問題に利用されるが，最大値，または最小値が求まるのは，相加平均，または相乗平均が定数になる場合であって，次のような使い方は正しくない：
例題 $x\!>\!0$ のとき，関数 $f(x)\!=\!x^2\!+\!\dfrac1x$ の最小値は?
こたえ（？？）
$x^2>0,\ \dfrac 1x>0$ であるから，相加・相乗平均の関係により， \[x^2+\frac1x\geqq2\sqrt{x^2\cdot\frac1x}=2\sqrt x\] 等号成立は，$x^2=\dfrac1x$，即ち $x^3=1$ のときだから，$x=1$．(ここまでは正しい．)
よって，$x^2+\dfrac1x\geqq2\sqrt 1=2$ より，最小値は2（？？）(← 正しくない．)
正しくは，$x=\dfrac1{\sqrt[3]2}$ で最小となる．
$x^2+\dfrac1x\geqq2\sqrt x$ という不等式は，関数としての大小関係が正しいうえに，$x^2+\dfrac1x=2\sqrt x$ となる $x$ が1であることも正しい．しかし，$x^2+\dfrac1x$ の最小値は2ではない．
因みに $x=\dfrac1{\sqrt[3]2}$ で最小となることを確かめるには，関数 $x^2+\dfrac1x$ を微分(数学Ⅲの内容)して増減を調べてみるのが簡単だが，次のように数学Ⅱの範囲の微分でも確認することができる．
$x^2+\dfrac1x=k\ (\cdots$①) とおく．$x>0$ のとき，$x^2+\dfrac1x$ のとる値が $k$ であるということは，逆に $x^2+\dfrac1x$ を $k$ にするような実数 $x$ が存在しているということ，即ち
$x^3+1=kx\ \ \cdots$ ②
を満たす実数 $x$ が存在しているということである．この同値な言いかえは，左辺の3次関数のグラフと右辺の原点を通る傾き $k(\,>0)$ 直線が共有点をもつことである．グラフをイメージすると，直線が3次関数のグラフと接するとき，$k$ の値は最小となる．3次関数のグラフ上の点 $(t,t^3+1)$ における接線の方程式は
\[y=3t^2(x-t)+t^3+1\]
これが原点を通るとき，
\[0=3t^2\cdot (-t)+t^3+1\ \ \therefore t=\frac1{\sqrt[3]2}\]
$x=\dfrac1{\sqrt[3]2}$ のとき①の値を $k_0$ とすれば，②で両辺のグラフが $x=\dfrac1{\sqrt[3]2}$ 以外で共有点をもとうとすると，$k>k_0$ となってしまう．よって関数 $x^2+\dfrac1x$ の最小値 $k_0$ を実現する $x$ の値は $\dfrac1{\sqrt[3]2}$ である．
このページで疑問は解決されましたか？
こちらから数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第1章 式と証明
| スライド | ノート | |
| 1. 整式の除法 | [無料] | |
| 2. 分数式 | [無料] | |
| 3. 恒等式 | [無料] | |
| 4. 等式の証明 | [無料] | |
| 5. 不等式の証明 | [無料] |