8. 定積分(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]

8.　定積分

8.1　定積分

　$F(x)$ を $f(x)=2x+1$ の不定積分とすると， $$F(x)=\int f(x)\,dx=x^2+x+C$$ 　ここで例えば， $$\begin{align*} F(3)-F(1)&=(3^2+3+C)-(1^2+1+C)\\[5pt] &=10 \end{align*}$$ と積分定数 $\boldsymbol{C}$ によらない値となる．

　一般に，関数 $f(x)$ の不定積分を $F(x)$ とするとき，$F(b)-F(a)$ は積分定数 $C$ によらない値となる．この $F(b)-F(a)$ を関数 $f(x)$ の $a$ から $b$ までの定積分といい， $$\int_a^b f(x)\,dx$$ で表す．また，$F(b)-F(a)$ を $$\Bigl[F(x)\Bigr]_a^b$$ とも書く：

定積分　関数$f(x)$の不定積分の1つを$F(x)$とするとき， $$\int_a^b\!f(x)dx\!=\!\Bigl[F(x)\Bigr]_a^b\!=\!F(b)\!-\!F(a)$$

補足1

　$\displaystyle\int_a^b f(x)\,dx$ について，$a$ を積分区間の下端，$b$ を積分区間の上端という．

補足2

　$a\!<\!b,a\!=\!b,a\!>\!b$ のいずれの場合でも $\displaystyle\int_a^b f(x)\,dx$ は意味を持つ．

例

$$\begin{align*} &\int_2^{-1}\!\!(x^2\!-\!x\!+\!1)dx\!=\!\left[\frac{x^3}3\!-\!\frac{x^2}2\!+\!x\right]_2^{-1}\\[5pt] \!=&\left\{\!\frac{(-1)^3}3\!-\!\frac{(-1)^2}2\!+\!(-1)\!\right\}\!-\!\left(\frac{2^3}3\!-\!\frac{2^2}2\!+\!2\right)\\[5pt] \!=&-\frac{11}6-\frac83\!=\!\underline{\boldsymbol{-\frac92}} \end{align*}$$

8.2　定積分の性質

定積分の性質1 $$\begin{align*} &[1]\ \int_a^b\!kf(x)\,dx\!=\!k\!\int_a^b\!f(x)\,dx\ (k\mbox{は定数})\\ &[2]\ \int_a^b\!\{f(x)\!+\!g(x)\}dx\!=\!\int_a^b\!\!f(x)dx\!+\!\!\int_a^b\!g(x)dx \end{align*}$$

証明

　$f(x),g(x)$ の不定積分の1つをそれぞれ $F(x),G(x)$ とする．

[1]

$$\begin{align*} \int_a^b kf(x)\,dx&=\Bigl[kF(x)\Bigr]_a^b\\[5pt] &=kF(b)-kF(a)\\[5pt] &=k\{F(b)-F(a)\}\\[5pt] &=k\int_a^b f(x)\,dx \end{align*}$$

[2]

$$\begin{align*} \int_a^b \{f(x)+g(x)\}\,dx&=\Bigl[F(x)+G(x)\Bigr]_a^b\\[5pt] &=\{F(b)+G(b)\}-\{F(a)+G(a)\}\\[5pt] &=\{F(b)-F(a)\}+\{G(b)-G(a)\}\\[5pt] &=\int_a^b f(x)\,dx+\int_a^b g(x)\,dx \end{align*}$$

■

例1

$$\begin{align*} \int_1^3 2x\,dx&=2\int_1^3 x\,dx\ \ (\gets\mbox{性質}[1])\\[5pt] &=2\Bigl[\frac{x^2}2\Bigr]_1^3\\[5pt] &=2\cdot\frac{3^2-1^2}2\\[5pt] &=\underline{\boldsymbol{8}} \end{align*}$$

例2

$$\begin{align*} &\int_{-1}^2 (x^2-x+1)\,dx\\[5pt] =&\int_{-1}^2 x^2\,dx-\int_{-1}^2 x\,dx+\int_{-1}^2 dx\ \ (\gets\mbox{性質}[2])\\[5pt] =&\Bigl[\frac{x^3}3\Bigr]_{-1}^2-\Bigl[\frac{x^2}2\Bigr]_{-1}^2+\Bigl[x\Bigr]_{-1}^2\\[5pt] =&\frac{2^3-(-1)^3}3-\frac{2^2-(-1)^2}2+\{2-(-1)\}\\[5pt] =&3-\frac32+3\\[5pt] =&\underline{\boldsymbol{\frac92}} \end{align*}$$

定積分の性質2 $$\begin{align*} &[3]\ \int_a^a\!\!f(x)dx\!=\!0\\ &[4]\ \int_b^a\!\!f(x)dx\!=\!-\int_a^b\!\!f(x)dx\\ &[5]\ \int_a^b\!\!f(x)dx\!=\!\int_a^c\!\!f(x)dx\!+\!\int_c^b\!\!f(x)dx \end{align*}$$

証明

　$f(x)$ の不定積分の1つを $F(x)$ とする．

[3]

$$\begin{align*} \int_a^a f(x)\,dx&=\Bigl[F(x)\Bigr]_a^a\\[5pt] &=F(a)-F(a)\\[5pt] &=0 \end{align*}$$

[4]

$$\begin{align*} \int_b^a f(x)\,dx&=\Bigl[F(x)\Bigr]_b^a\\[5pt] &=F(a)-F(b)\\[5pt] &=-\{F(b)-F(a)\}\\[5pt] &=-\int_a^b f(x)\,dx \end{align*}$$

[5]

$$\begin{align*} (\mbox{右辺})&=\Bigl[F(x)\Bigr]_a^c+\Bigl[F(x)\Bigr]_c^b\\[5pt] &=\{F(c)-F(a)\}+\{F(b)-F(c)\}\\[5pt] &=F(b)-F(a)\\[5pt] &=\int_a^b f(x)\,dx\\[5pt] &=(\mbox{左辺}) \end{align*}$$

■

例

$$\begin{align*} \int_2^{-1}\!\!\!\!x\,dx-\int_3^{-1}\!\!x\,dx&=\int_2^{-1}\!\!\!\!x\,dx+\int_{-1}^3\!\!x\,dx\ \ (\gets\mbox{性質}[4])\\[5pt] &=\int_2^3\!\!x\,dx\ \ (\gets\mbox{性質}[5])\\[5pt] &=\left[\frac{x^2}2\right]_2^3\\[5pt] &=\underline{\boldsymbol{\frac52}} \end{align*}$$

8.3　定積分を含む関数

例題　$f(x)\!=\!x^2\!-\!3x\!+\!{\displaystyle\int_0^2}\!\!f(t)\,dt$ のとき，$f(x)$ を求めよ．

ポイント
　式中の定積分を $a$ (定数)とおいて，定積分を含まぬ形にする．
　↓
　$a$ とおいた定積分を計算．

答

　　$\displaystyle \int_0^2f(t)\,dt$ を $a$ (定数)とおくと，

$f(x)=x^2-3x+a\ \ \cdots$①

(一見，積分を含んだいかめしい形の与式は，単なる2次関数であったのだ．)

　$a$ とおいた定積分を計算すると， $$\begin{align*} a&=\int_0^2 f(t)\,dt\\[5pt] &=\int_0^2(t^2-3t+a)\,dt\ \ (\because\mbox{①})\\[5pt] &=\Bigl[\frac{t^3}3-\frac32t^2+at\Bigr]_0^2\\[5pt] &=\frac83-6+2a\\[5pt] &=-\frac{10}3+2a \end{align*}$$

　従って，

$$\begin{align*} a&=-\frac{10}3+2a\\[5pt] \therefore a&=\frac{10}3 \end{align*}$$ 　よって①より， $$\underline{\boldsymbol{f(x)=x^2-3x+\frac{10}3}}$$

注意

　例えば，$f(x)=x^2+\displaystyle\int_0^1\!\!x\,tf(t)\,dt$ のとき，

$\displaystyle\int_0^1\!\!x\,tf(t)\,dt=a$ (定数)とおく．

としてはいけない．何故なら $x=p$ のとき $f(x)$ は $f(p)=p^2+\displaystyle\int_0^1p\,tf(t)\,dt$ となるが，$\displaystyle\int_0^1p\,tf(t)\,dt$ の部分は $x$ の値 $p$ によって変化し，定数ではないからである．このような場合の対処法は，積分変数 $t$ 以外の文字は定数とみなして

$$f(x)=x^2+x\int_0^1\!\!tf(t)\,dt$$

と $x$ を定積分の前に出し，

$\displaystyle\int_0^1\!\!tf(t)\,dt=a$ (定数)とおく．

とするのである．

8.4　定積分と微分法

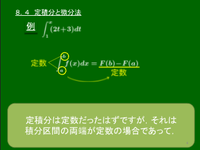
例題　$\displaystyle\frac d{dx}\int_1^x (2t+3)\,dt$ を計算せよ．

※ $\dfrac{d}{dx}f(x)$ のような表記の意味についてはこちら．

答

$$\begin{align*} \int_1^x (2t+3)\,dt&=\Bigl[t^2+3t\Bigr]_1^x\\[5pt] &=x^2+3x-4 \end{align*}$$

　よって，$\displaystyle\int_1^x (2t+3)\,dt$ は $x$ の2次関数である．この関数を $x$ で微分するのであるから，

$$\begin{align*} \frac d{dx}\int_1^x(2t+3)\,dt&=\frac d{dx}(x^2+3x-4)\\[5pt] &=2x+3 \end{align*}$$

　これは，$\displaystyle\int_1^x (2t+3)\,dt$ の被積分関数 $2t+3$ の $t$ を $x$ に置き換えたものである．

　一般に次が成り立つ：

$$\frac d{dx}\int_a^x\!\!f(t)dt=f(x)\ \ (a\,\mbox{は定数})$$

証明

　$f(x)$ の不定積分の1つを $F(x)$ とする．(即ち，$F'(x)=f(x)$ )

$$\begin{align*} \int_a^x f(t)\,dt&=\Bigl[F(t)\Bigr]_a^x\\[5pt] &=F(x)-F(a) \end{align*}$$

　よって，

$$\begin{align*} \frac d{dx}\int_a^x f(t)\,dt&=\frac d{dx}\{F(x)-F(a)\}\\[5pt] &=\frac d{dx}F(x)-\frac d{dx}F(a)\\[5pt] &=f(x) \end{align*}$$

■

補足

①　$\displaystyle\int_a^x f(t)\,dt$ は微分すると $f(x)$ になるから，$f(x)$ の1つの不定積分である．

②　$\displaystyle\int_a^x f(t)\,dt$ は $x=a$ のとき， $$\int_a^a f(t)\,dt=0\ \ (\gets \mbox{性質3})$$

③　上の証明から $a$ は定数であればどんな値でもよい．

例題　等式 $\displaystyle\int_a^x\!\!f(t)\,dt\!=\!x^2\!-\!3x\!+\!a$ を満たす関数 $f(x)$ と $a$ の値を求めよ．

答

　与式の両辺を微分すると

$$\frac d{dx}\int_a^x f(t)\,dt=\frac d{dx}(x^2-3x+a)$$

$$\therefore \underline{\boldsymbol{f(x)=2x-3}}$$

　また，与式の両辺の $x$ を $a$ とおくと，

$$\begin{align*} \int_a^a f(t)\,dt&=a^2-3a+a\\ &=a^2-2a\\[5pt] &=a(a-2)\\[5pt] \therefore 0&=a(a-2) \end{align*}$$

$$\therefore \underline{\boldsymbol{a=0,2}}$$

---

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]