3次以上の方程式では,解いて解を求めるというのは時として容易ではありません.しかし,微分して関数の増減を調べることで,その方程式がもつ解のいくつかの情報を取り出すことが可能です.
不等式の証明では,(左辺)-(右辺)を計算する,及び相加・相乗平均の関係など有名不等式を利用するという方法がありました.微分を用いれば,複雑な不等式を証明できる場合があります.
高校数学[総目次]
数学Ⅱ 第6章 微分法・積分法
| スライド | ノート | 問題 | |
| 1. 微分係数 | [無料] | ||
| 2. 導関数 | [無料] | ||
| 3. 接線 | [会員] | [会員] | |
| 4. 関数の値の変化 | [会員] | [会員] | |
| 5. 極大・極小 | [会員] | ||
| 6. 関数のグラフと方程式・不等式 | [会員] |
| 7. 不定積分 | [無料] | ||
| 8. 定積分 | [会員] | ||
| 9. 様々な定積分 | [会員] | ||
| 10. 面積 | [会員] |

| 6.1 グラフと方程式の関係 6.2 関数のグラフと方程式 |
スライド① |
| 6.2 関数のグラフと不等式 | スライド② |
スライドはぜひ全画面表示で
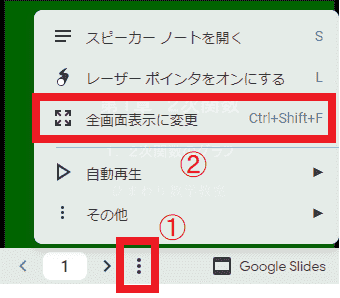
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
