4. 関数の値の変化(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]

4.　関数の値の変化

4.1　単調性

　実数の集合 $\{x|a\leqq x\leqq b\}$ や，$\{x|a<x<b\}$ などを区間という．

　ある区間において，区間内の任意の $x_1, x_2$ について，

$$x_1<x_2\ \Longrightarrow \ f(x_1)<f(x_2)$$

が成り立つとき，$f(x)$ はその区間で単調に増加するという．

　同様に，ある区間において，

$$x_1<x_2\ \Longrightarrow \ f(x_1)>f(x_2)$$

が成り立つとき，$f(x)$ はその区間で単調に減少するという．

　例えば関数 $y=x^2$ は，$x\leqq0$ において単調に減少し，$x\geqq0$ において単調に増加する．

　単調性はグラフを考えるとわかりやすい．単調に増加する $x$ の区間ではグラフが右上がりで，単調に減少する $x$ の区間ではグラフは右下がりである．

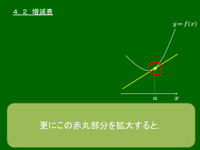
4.2　増減表

　関数 $f(x)$ の導関数 $f'(x)$ は，$f(x)$ のグラフについて接線の傾きの情報を与えていた．ある $x$ の区間で接線の傾きが常に正であれば，$f(x)$ のグラフはその区間で右上がりとなっているし，逆に接線の傾きが負となる区間では $f(x)$ のグラフは右下がりとなっている．従って次が成り立つ：

　　ある区間で常に $f'(x)>0$
　　　　$\Longrightarrow\ \ f(x)$ はその区間で単調に増加する
　　ある区間で常に $f'(x)<0$
　　　　$\Longrightarrow\ \ f(x)$ はその区間で単調に減少する
　　ある区間で常に $f'(x)=0$
　　　　$\Longrightarrow\ \ f(x)$ はその区間で定数である

　つまり

$\boldsymbol{f'(x)}$ の符号を見れば，関数の増減がわかる

ということである．

補足

　　直感的にわかり易い内容であるが，厳密には証明が必要．詳しくは数学Ⅲの微分 9．関数の値の変化 を参照．

例題　関数 $y=x^2$ の増減を調べよ．

答

　$y’=2x$ により，$y’=0$ のとき $x=0$．

　$x$ の区間ごとの $y’$ や $y$ を次のような表にまとめるとわかりやすい：

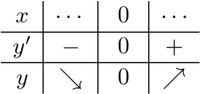
　この表を関数の増減表という．

　この増減表により
　　　$x\leqq0$ で単調に減少する．
　　　$x\geqq0$ で単調に増加する．

補足

　境界である $x=0$ は単調増加にも単調減少にも含める．(詳しくは数学Ⅲの微分法における関数の値の変化 を参照．)

---

高校数学[総目次]

数学Ⅱ　第6章　微分法・積分法

	スライド	ノート	問題
1. 微分係数	[無料]
2. 導関数	[無料]
3. 接線	[会員]		[会員]
4. 関数の値の変化	[会員]		[会員]
5. 極大・極小	[会員]
6. 関数のグラフと方程式・不等式	[会員]

7. 不定積分	[無料]
8. 定積分	[会員]
9. 様々な定積分	[会員]
10. 面積	[会員]