微分係数は「 における微分係数」といったように,各 の値毎に定められる量です. における微分係数は の関数となります.そこで文字を から に変えた関数を,元の関数の導関数といい,導関数を求めることを「微分する」といいます.
まず, の導関数の公式を確認しますが,この公式が微分におけるもっとも基本的な公式となります.
次に,一般の関数の導関数において成り立つ性質を確認します.
高校数学(総目次)
数学Ⅱ 第6章 微分法・積分法
| スライド | ノート | 問題 | |
| 1. 微分係数 | [無料] | ||
| 2. 導関数 | [無料] | ||
| 3. 接線 | [会員] | [会員] | |
| 4. 関数の値の変化 | [会員] | [会員] | |
| 5. 極大・極小 | [会員] | ||
| 6. 関数のグラフと方程式・不等式 | [会員] |
| 7. 不定積分 | [無料] | ||
| 8. 定積分 | [会員] | ||
| 9. 様々な定積分 | [会員] | ||
| 10. 面積 | [会員] |

2.導関数
| 2.1 導関数 | スライド① |
| 2.2 の導関数 2.3 導関数の性質 | スライド② |
スライドはぜひ全画面表示で
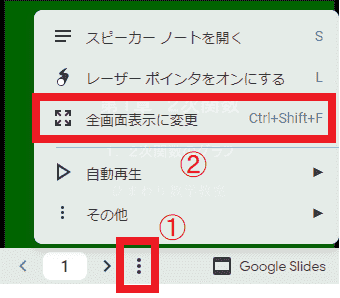
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
スライド① 導関数
スライド② の導関数,導関数の性質

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学(総目次)
数学Ⅱ 第6章 微分法・積分法
| スライド | ノート | 問題 | |
| 1. 微分係数 | [無料] | ||
| 2. 導関数 | [無料] | ||
| 3. 接線 | [会員] | [会員] | |
| 4. 関数の値の変化 | [会員] | [会員] | |
| 5. 極大・極小 | [会員] | ||
| 6. 関数のグラフと方程式・不等式 | [会員] |
| 7. 不定積分 | [無料] | ||
| 8. 定積分 | [会員] | ||
| 9. 様々な定積分 | [会員] | ||
| 10. 面積 | [会員] |
