高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | [会員] | ||
| 2. 複素数が表す図形 | [会員] | ||
| 3. 極形式 | [会員] | [会員] | |
| 4. ド・モアブルの定理 | [会員] | ||
| 5. 複素数と図形 | [会員] |

5. 複素数と図形
5.1 線分の内分点,外分点
平面ベクトルのときと全く同じ考え方により,複素平面での内分点,外分点は次のように表される:
2点A(α),B(β) について,線分ABを m:nに内分する点: nα+mβm+nm:nに外分する点: −nα+mβm−n
補足
[ベクトルでは次のようであった.]
A(→(a),B(→(b) について,線分ABを
m:n に内分する点の位置ベクトル:n→(a+m→(bm+n
m:n に外分する点の位置ベクトル:−n→(a+m→(bm−n

5.2 方程式の表す図形
円
円とは,中心と呼ばれる1点から等しい距離にある点の集合であるから,その方程式は次のように表される:
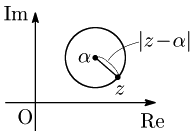
点 α を中心とする半径 r の円の方程式 |z−α|=r⟺(z−α)(¯z−¯α)=r2⟺z¯z−¯αz−α¯z=r2−|α|2
垂直二等分線
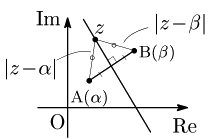
線分ABの垂直二等分線とは,線分ABの両端から等しい距離にある点の集合であるから,その方程式は次のように表される:
A(α),B(β) のとき,線分ABの垂直二等分線の方程式 |z−α|=|z−β|

5.3 半直線のなす角
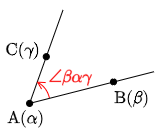
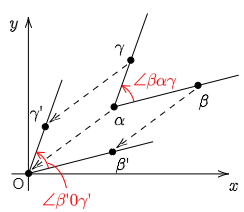
図において,半直線ABからACまでの回転角を ∠βαγ で表す.極形式 での偏角と同様に,反時計回りの回転角を正の向き,時計回りを負の向きとする.
極形式のところで学んだ,argz1z2=argz1−argz2 を上の場合に適用することを考えよう.A(α) が極Oにくるような平行移動を考えたとき,点B(β), C(γ) は,それぞれ点B′(β′), C′(γ′) に移ったとすると,
{β′=β−αγ′=γ−α …①
である.
よって
∠βαγ=∠β′0γ′=argγ′−argβ′=argγ′β′=argγ−αβ−α (∵①)
となる.
異なる3点 α, β, γ について, ∠βαγ=argγ−αβ−α
注意
文字の順番に注意.∠γαβ だと角の大きさは上の図と同じだが,向きが逆になる.
異なる3点が1直線上にあるための条件
異なる3点 α,β,γ が1直線上
⟺∠βαγ=0 又は π
⟺argγ−αβ−α=0 又は π
⟺γ−αβ−α は実数
垂直条件
A(α),B(β),C(γ) について,
AB⊥AC
⟺∠βαγ=π2 又は −π2
⟺argγ−αβ−α=π2 又は −π2
⟺γ−αβ−α は純虚数
【発展】4点が同一円周上にあるための条件
異なる4点 A(α),B(β),C(γ),D(δ) のうち,どの3点も同一直線上にないとする.つまりこの4点を使って四角形ができる場合である.このとき,この4点が同一円周上にあるための条件を求めよう.
この4点のうち,CとDは直線ABに関して同じ側にあるか,反対側にあるかどちらかである.
1° CとDが直線ABに関して同じ側にあるとき
4点が同一円周上
⟺ ∠ACB=∠ADB …①
⟺ ∠αγβ=∠αδβ …②
⟺ argβ−γα−γ−argβ−δα−δ=0
⟺ arg(β−γα−γ÷β−δα−δ)=0
⟺ β−γα−γ÷β−δα−δ は正の実数
式を追う上での補足
①では角の大きさだけで向きはない.②では回転の向きが正負で表されるが,CとDの位置関係によらず,両辺とも同符号である.
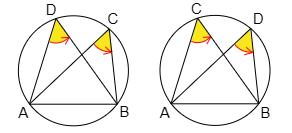
いずれの場合も②の両辺は同符号となる.
2° CとDが直線ABに関して反対側にあるとき
円に内接する四角形 の条件により
4点が同一円周上
⟺ ∠ACB+∠BDA=π …③
⟺ ∠αγβ+∠βδα=±π …④
⟺ argβ−γα−γ+argα−δβ−δ=±π
⟺ arg(β−γα−γ×α−δβ−δ)=±π
⟺ arg(β−γα−γ÷β−δα−δ)=±π
⟺ β−γα−γ÷β−δα−δ は負の実数
式を追う上での補足
③では角の大きさだけで向きはない.④では ∠αγβ と ∠βδα は回転の向きが同じで,反時計回りだと +πに,時計回りだと −π になっている.(③で∠ADBではなく,∠BDAとなっているのは回転の向きをそろえるためである.)
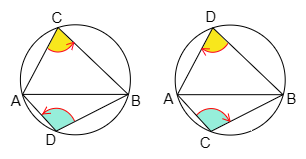
1°,2° により,次が成り立つ:
4点が同一円周上にあるための条件 異なる4点 A(α),B(β),C(γ),D(δ) のうち,どの3点も同一直線上にないとする.このとき
4点が同一円周上にある
⟺ β−γα−γ÷β−δα−δ が実数

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | [会員] | ||
| 2. 複素数が表す図形 | [会員] | ||
| 3. 極形式 | [会員] | [会員] | |
| 4. ド・モアブルの定理 | [会員] | ||
| 5. 複素数と図形 | [会員] |