高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | [会員] | ||
| 2. 複素数が表す図形 | [会員] | ||
| 3. 極形式 | [会員] | [会員] | |
| 4. ド・モアブルの定理 | [会員] | ||
| 5. 複素数と図形 | [会員] |

3. 極形式
3.1 極形式とは
複素数の新しい表現法~具体例
例えば,複素数 z=1+√3i は複素平面上で次の点を表す.
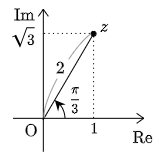
この実部の 1 と虚部の √3 は,三角関数のところで学んだように原点からの距離2と実軸からの回転角 π3 によって
1=2cosπ3, √3=2sinπ3
というようにも表すことができるから
z=2cosπ3+(2sinπ3)i
とも表現できる.2でくくって
z=2(cosπ3+isinπ3)
これが複素数 z の新しい表現法である.つまりこの複素数 z は
1+√3=2(cosπ3+isinπ3)
という2通りの表し方ができるようになったのだ.
複素数の新しい表現法~一般論
a, b を実数として,複素平面上の原点O以外の点 z=a+bi は次のような点を表すのであった.
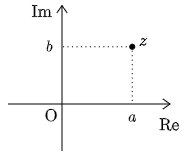
今この実部と虚部である a, b を異なる方法で表すことを考える.そうすることで,複素数の取り扱いが驚くほど簡単になる上に,複素平面において,回転移動という変換がとても考えやすくなるのである.

複素平面上の原点O以外の点 z を,Oからの距離 r と,実軸の正の向きからの回転角 θ で表すことを考える.ただし,反時計回りを正の向き,時計回りを負の向きとし,角度は弧度法 を用いる.
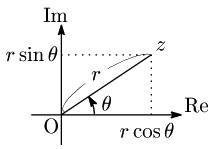
図から複素数 z の実部は rcosθ,虚部は rsinθ と表されることがわかる.この辺りの考え方は三角関数のところで十分習熟していることであろう.従って z は
z=rcosθ+irsinθ
と表せる.r でくくって
z=r(cosθ+isinθ)
複素数のこのような表し方を極形式(きょくけいしき)という.
極形式 z=r(cosθ+isinθ)
i が + のすぐあとにきているのが気になるかもしれないが,これは z=r(cosθ+sinθi) と書いたのでは,sin(θi) と紛らわしいため,通常このような記法をとる.どうしても i を最後に書きたい場合は,(sinθ)i のように i が sinθ の中に入っていないことがはっきりとわかるように書かなくてはならない.
このときの角 θ を偏角(へんかく)といい,argz で表す.
arg z=θ
この arg というのは英語で偏角を意味する argument からきている.
また,複素数 z の絶対値 |z| は,複素平面上において原点からの距離を表していたから
|z|=r
である.これは計算によっても
|z|=|r|√cos2θ+sin2θ=|r|=r
となることから確かめられる.
まとめr=|z|, θ=argz
補足
例えば,arg(1−i) は 74π でも −π4 でもよい.つまり,2π の整数倍の差がある2つを同一視する.
argz1=argz2 というときは,2π の整数倍の違いを無視して一致することを意味する.
例
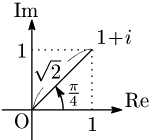
z=1+i のとき,|z|=√2,argz=π4 により, z=√2(cosπ4+isinπ4)
例題 複素数 z が極形式で z=r(cosθ+isinθ) と表されているとき, z の共役 ¯z を極形式で表せ.
こたえ
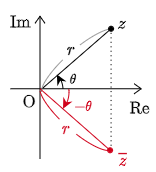
図より,
|¯z|=r, arg¯z=−θ
であるから
¯z=r{cos(−θ)+isin(−θ)}
z が実数や純虚数となる条件
複素数 z が実数や純虚数となる条件を,偏角という観点から見ていこう.ただし,偏角 θ は 0≦θ<2π とする.
複素平面上において,
z が実数 ⟺z は実軸上
であったから,実軸上にある複素数の偏角は,原点を除き 0 か π である.
また,z が0でなければ
z が純虚数 ⟺z は虚軸上
であったから,虚軸上にある複素数の偏角は,原点を除き π2 か 32π である.
定理 0でない複素数 z について,偏角が0以上 2π 未満のとき
z が実数 ⟺ arg z=0 or π
z が純虚数 ⟺ arg z=π2 or 32π

3.2 複素数の乗法・除法
次の例題を考えてみよう.
例題 2つの複素数 z1=1+√3i,z2=1+i について,z1z2,z1z2 をそれぞれ極形式で表せ.
z1z2 から考えていこう.これを極形式で表すには z1z2 という複素数について,原点からの距離,すなわち |z1z2| と,偏角 arg z1z2 の情報が必要である.z1z2 を実際に計算してみると
z1z2=(1+√3i)(1+i)=(1−√3)+(1+√3)i
となるから
|z1z2|=√(1−√3)2+(1+√3)2=√8=2√2
である.一方,偏角 arg z1z2 の方はというと,下の図のように複素平面上に点 z1z2 を何となくとってみても,偏角はよくわからない.
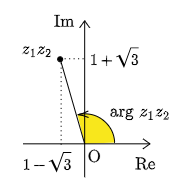
これ以上はお手上げになってしまった.
極形式なら打開できる
上の例題では z1z2 の絶対値は計算できても,偏角の方がよくわからず,結局 z1z2 を極形式で表すことは叶わなかった.ところが実は z1 と z2 を最初の段階で極形式で表しておけば,事態が打開できるのである.
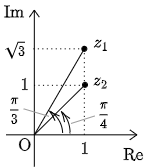
z1, z2 をそれぞれ極形式で表すと,
z1=2(cosπ3+isinπ3)z2=√2(cosπ4+isinπ4)
と表されるから,
z1z2=2(cosπ3+isinπ3)⋅√2(cosπ4+isinπ4)=2√2{(cosπ3cosπ4−sinπ3sinπ4_①)+(sinπ3cosπ4+cosπ3sinπ4_②)i}
となる.ところで①式は,cosの加法定理により
①=cos(π3+π4)=cos712π
同様に②式も,sinの加法定理により
②=sin(π3+π4)=sin712π
となるから,結局
z1z2=2√2(cos712π+isin712π)_
という具合に極形式で表すことができた.複素数 z1z2 の偏角は 712π(=105∘) なので,やはり図から偏角を求めるのは難しいといえる.
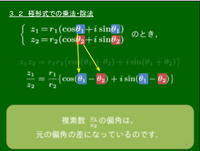
極形式による積や商の一般論
例題の商の計算が残っているが,ここで中断して,極形式による積や商の一般論を展開する.
2つの複素数 z1, z2 が極形式で
z1=r1(cosθ1+isinθ1), z2=r2(cosθ2+isinθ2)
と表されているとする.
● 積
z1z2=r1r2(cosθ1+isinθ1)(cosθ2+isinθ2)=r1r2{cosθ1cosθ2−sinθ1sinθ2)+i(sinθ1cosθ2+cosθ1sinθ2)}=r1r2{cos(θ1+θ2)+isin(θ1+θ2)}
であるから,
|z1z2|=|r1r2|√cos2(θ1+θ2)+sin2(θ1+θ2)=|r1||r2|=|z1||z2|argz1z2=argz1+argz2
● 商
z1z2=r1(cosθ1+isinθ1)r2(cosθ2+isinθ2)=r1r2⋅(cosθ1+isinθ1)(cosθ2−isinθ2)(cosθ2+isinθ2)(cosθ2−isinθ2)=r1r2⋅(cosθ1+isinθ1)(cosθ2−isinθ2)1=r1r2⋅(cosθ1+isinθ1)(cosθ2−isinθ2)=r1r2⋅{(cosθ1cosθ2+sinθ1sinθ2)+i(sinθ1cosθ2−cosθ1sinθ2)}=r1r2{cos(θ1−θ2)+isin(θ1−θ2)}
であるから,
|z1z2|=|r1r2|=|r1||r2|=|z1||z2|argz1z2=θ1−θ2=argz1−argz2
以上をまとめると次のようになる.
まとめ|z1z2|=|z1||z2|arg z1z2=arg z1+arg z2|z1z2|=|z1||z2|argz1z2=arg z1−arg z2
これを言葉で大雑把に表現すると次のようになる.
まとめ 2つの複素数 z1, z2 について
積 z1z2 の絶対値は,それぞれの絶対値の積
積 z1z2 の偏角は,それぞれの偏角の和
商 z1z2 の絶対値は,それぞれの絶対値の商
商 z1z2 の偏角は,それぞれの偏角の差
戻って例題の解説
一般論がわかったので,残っていた例題の商は
|z1z2|=|z1||z2|=2√2=√2arg z1z2=arg z1−arg z2=π3−π4=π12
よって z1z2 の極形式は
z1z2=√2(cosπ12+isinπ12)_
これで無事,商の方も解決できた.
3.3 拡大・縮小と回転移動
極形式で表された2つの複素数の積や商がどのようになるかを詳しく見たが,これを図形の変換という立場から捉え直してみよう.
前節の例題で用いた2つの複素数 z1, z2 をもう一度取り上げよう.
z1=2(cosπ3+isinπ3)z2=√2(cosπ4+isinπ4)
ここで,点 z1 を主役にして,この z1 に z2 を掛けると,z1 がどのように変化するかという立場で眺めてみよう.
|z1|=2, arg z1=π3
であった.z1 に z2 を掛けると,
|z1z2|=|z1|×|z2|=2×√2arg z1z2=arg z1+arg z2=π3+π4
となるから,z1 は
- 絶対値が |z2| 倍される.
- 偏角が arg z2 だけ足される.
という変換が施されたと解釈できる.特に偏角の方は,z2 を掛けることで
原点を中心に arg z2 だけ回転移動を行う
と言い換えることができるのである.このように,ある複素数 z に別の複素数を掛けるという行為は,z に対して
拡大・縮小と,回転移動を同時に行う変換を施している
ということを意味するのだ.
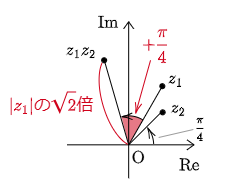
補足 今は z1 を主役に考えたが,複素数の積は交換法則が成り立つから,主従を逆転させて,「z2 に z1 を掛けると,z2 の絶対値は |z1| 倍され,更に原点を中心として π3 の回転移動を行う変換が施される」という解釈ももちろんできる.
掛ける複素数の絶対値が1なら回転移動だけ
上の例では |z2|=√2 であったから,積 z1z2 は拡大と回転移動の2つの変換が行われたが,絶対値が1である複素数を掛けたときは,拡大倍率が1だから原点からの距離が変化せず,回転移動だけの変換となる.
絶対値が1で偏角が θ である複素数は,極形式で 1(cosθ+isinθ) と表されるから次が成り立つ.
回転移動を表す複素数原点を中心として角 θ の回転移動を表す複素数はcosθ+isinθ

例題 複素平面上の点 z=1+√3i を,原点を中心として π4 だけ回転移動させた点を表す複素数を求めよ.
こたえ
原点を中心とする π4 の回転移動を表す複素数は
cosπ4+isinπ4=√22+√22i
である.よって求める複素数は
(1+√3i)(√22+√22i)=−√6−√22+√6+√22i_

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | [会員] | ||
| 2. 複素数が表す図形 | [会員] | ||
| 3. 極形式 | [会員] | [会員] | |
| 4. ド・モアブルの定理 | [会員] | ||
| 5. 複素数と図形 | [会員] |