2. 複素数が表す図形(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート	問題
1. 複素平面	[会員]
2. 複素数が表す図形	[会員]
3. 極形式	[会員]		[会員]
4. ド・モアブルの定理	[会員]
5. 複素数と図形	[会員]

2. 複素数が表す図形

　このノートでは特に断らない限り，$a+b\,i$ などと書けば，$a,\ b$ は実数であるとする．また，$z,\ \alpha,\ \beta,\ \gamma$ などの文字を断りなく複素数として記述することがある．

2.1　複素数の実数倍

　複素平面上の点 $\alpha\ (=a+b\,i)$ に対して，実数倍 $t\,\alpha$ ($t$ は実数)は次のような点を表す：

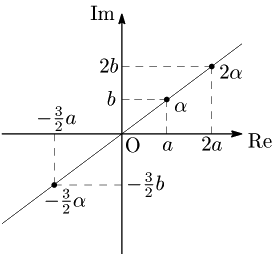
　このことから一般に次が成り立つ．

定理　$\alpha\neq0$ のとき
　　　　複素平面上の3点 $0,\ \alpha,\ \beta$ が一直線上にある
　　$\iff \beta=k\alpha$ を満たす実数 $k$ が存在する

例題　3点 $0,\ 2+3\,i,\ 8+b\,i$ が一直線上にあるとき，$b$ の値を求めよ．

　解答例を表示する

　3点 $0,\ 2+3\,i,\ 8+b\,i$ が一直線上にあるから実数 $k$ を用いて $$8+b\,i=k(2+3\,i)$$ と表される．故に $$8=2k,\ b=3k$$ $$\therefore k=4$$ 　よって $b=3\times4=12$

補足

　$\alpha$ を$\overrightarrow{\alpha}$と思えば，平面ベクトルの場合と同じである．

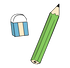
2.2　共役な複素数（complex conjugate 複素共役）

　複素数 $\alpha=a+b\,i$ に対して，$a-b\,i$ を $\alpha$ の共役な複素数(共役複素数・複素共役complex conjugate)といい，$\overline{\alpha}$ で表す．

補足

　$\alpha=a+b\,i$ のとき，$\overline{\alpha}=a-bi$ で，さらにこの共役は $$\overline{\overline{\alpha}}=\overline{a-b\,i}=a+b\,i$$ 　従って共役の共役は元の数である．

$$\overline{\overline{\alpha}}=\alpha$$

　複素平面上の点 $\alpha$ に対して，実軸・虚軸・原点に関して対称移動した点がそれぞれどのように表されるかを実軸→原点→虚軸の順に見ていく．

• 実軸に関する対称移動
  $\alpha=a+b\,i$ を実軸に関して対称移動した点は $a-b\,i$ となるから $\overline{\alpha}$ で表される．
• 原点に関して対称移動
  $\alpha=a+b\,i$ を原点に関して対称移動した点は $-a-b\,i(=-(a+b\,i))$ となるから $-\alpha$ で表される．
• 虚軸に関する対称移動
  $\alpha=a+b\,i$ を虚軸に関して対称移動した点は $-a+b\,i$ で，これは $\overline{\alpha}$ と原点に関して対称な点だから $-\overline{\alpha}$ で表される．

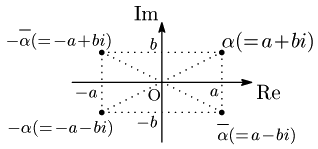
まとめ　複素平面上の点 $\alpha$ に対して
　　実軸に関して対称移動した点は　$\hspace{3mm}\overline{\alpha}$
　　虚軸に関して対称移動した点は　$-\overline{\alpha}$
　　原点に関して対称移動した点は　$-\alpha$

　複素数 $\alpha$ が実数であることは，複素平面上において $\alpha$ が実軸上にあることと同値であり，これは更に $\alpha$ は実軸に関して対称移動しても同じ複素数を表すことと同値である．従って $\overline{\alpha}=\alpha$ である．

　また複素数 $\alpha$ が純虚数であることは，複素平面上において $\alpha$ が虚軸上にあって，かつ $\alpha$ が0でないことと同値である．これは更に0でない複素数 $\alpha$ を虚軸に関して対称移動しても同じ複素数を表すことと同値である．従って $\overline{\alpha}=-\alpha$ である．

定理 　複素数 $\alpha$ について，
　　$\alpha$ が実数　 $\iff$ $\overline{\alpha}=\alpha$
　　$\alpha$ が純虚数 $\iff$ $\overline{\alpha}=-\alpha,\ \alpha\neq 0$

別の考え方

　$\alpha=a+b\,i$ とすると， $$\left\{ \begin{array}{ll} \alpha=a+b\,i&\cdots\mbox{①}\\[5pt] \overline{\alpha}=a-b\,i&\cdots\mbox{②} \end{array}\right.$$ 　(①$+$②)$\div2$ より，

$a=\dfrac{\alpha+\overline{\alpha}}2$

　(①$-$②)$\div2\,i$ より，

$b=\dfrac{\alpha-\overline{\alpha}}{2\,i}$

　従って，

$\alpha$ が実数　$\iff b\!=\!0\iff \dfrac{\alpha\!-\!\overline{\alpha}}{2\,i}\!=\!0\iff \overline{\alpha}\!=\!\alpha$

　また，$\alpha\neq0$ ならば，

$\alpha$ が純虚数$\iff a\!=\!0\iff \dfrac{\alpha\!+\!\overline{\alpha}}2\!=\!0\iff \overline{\alpha}\!=\!-\alpha$

■

補足

　証明中の囲み書きにある実部と虚部を表す式は，今後しばしば利用される：

　$\alpha=a+b\,i$ のとき， $$a=\frac{\alpha+\overline{\alpha}}2,\ \ \ \ b=\frac{\alpha-\overline{\alpha}}{2\,i}$$

2.3　共役な複素数の性質

　①　$\overline{\alpha+\beta}=\overline{\alpha}+\overline{\beta}$
　②　$\overline{\alpha-\beta}=\overline{\alpha}-\overline{\beta}$
　③　$\overline{\alpha\beta}=\overline{\mathstrut \alpha}\,\overline{\beta}$
　④　$\overline{\left(\dfrac \alpha \beta\right)}=\dfrac{\overline{\alpha}}{\overline{\beta}}$

証明

　$\alpha=a+b\,i,\ \beta=c+d\,i$ とする．

① $$\begin{align*} \mbox{左辺}&=\overline{(a+b\,i)+(c+d\,i)}\\[5pt] &=\overline{a+c+(b+d)i}\\[5pt] &=a+c-(b+d)i\\[5pt] \mbox{右辺}&=\overline{(a+b\,i)}+\overline{(c+d\,i)}\\[5pt] &=(a-b\,i)+(c-d\,i)\\[5pt] &=a+c-(b+d)i \end{align*}$$ 　よって(左辺)=(右辺)

② $$\begin{align*} \mbox{左辺}&=\overline{(a+b\,i)-(c+d\,i)}\\[5pt] &=\overline{a-c+(b-d)i}\\[5pt] &=a-c-(b-d)i\\[5pt] \mbox{右辺}&=\overline{(a+b\,i)}-\overline{(c+d\,i)}\\[5pt] &=(a-b\,i)-(c-d\,i)\\[5pt] &=a-c-(b-d)i \end{align*}$$ 　よって(左辺)=(右辺)

③ $$\begin{align*} \mbox{左辺}&=\overline{(a+b\,i)(c+d\,i)}\\[5pt] &=\overline{ac-bd+(ad+bc)i}\\[5pt] &=ac-bd-(ad+bc)i\\[5pt] \mbox{右辺}&=\overline{(a+b\,i)}\ \ \overline{(c+d\,i)}\\[5pt] &=(a-b\,i)\ \ (c-d\,i)\\[5pt] &=ac-bd-(ad+bc)i \end{align*}$$ 　よって(左辺)=(右辺)

④

　$\overline{\left(\dfrac\alpha\beta\cdot \beta\right)}$ は $\beta$ を約分すれば $\overline{\alpha}$ (…①)．

　一方，性質③より

$\overline{\left(\dfrac\alpha\beta\cdot\beta\right)}=\overline{\left(\dfrac\alpha\beta\right)}\ \overline{\beta}$ …②

　①，②より

$\overline{\alpha}=\overline{\left(\dfrac\alpha\beta\right)}\ \overline{\beta}$

　両辺を $\overline{\beta}(\neq0)$ で割って両辺を入れ替えると

$\overline{\left(\dfrac \alpha \beta\right)}=\dfrac{\overline{\alpha}}{\overline{\beta}}$

■

補足

　③で $\beta$ も $\alpha$ とおくと，$\overline{\alpha^2}=\left(\overline{\alpha}\right)^2$．
　従って帰納的に $n$ が自然数のとき，$\overline{\alpha^n}=\left(\overline{\alpha}\right)^n$．

$\overline{\alpha^n}=\left(\overline{\alpha}\right)^n$

例題　$a$ ～ $d$ は実数とする．方程式 $ax^3+bx^2+cx+d=0$ が $\alpha$ を解にもつならば，$\overline{\alpha}$ もこの方程式の解であることを示せ．

　解答例を表示する

　$\alpha$ が解であるから $$a\alpha^3+b\alpha^2+c\alpha+d=0$$ が成り立つ．この両辺の共役をとると $$\overline{a\alpha^3+b\alpha^2+c\alpha+d}=\overline{0}$$ 　上の定理により実数の共役複素数はその実数自身であるから右辺は0．また左辺は上の性質①を用いて書き換えると $$\overline{a\alpha^3}+\overline{b\alpha^2}+\overline{\mathstrut{c\alpha}}+\overline{d}=0$$ 　上の性質③により $$\overline{\mathstrut{a}}\,\overline{\alpha^3}+\overline{\mathstrut{b}}\,\overline{\alpha^2}+\overline{\mathstrut{c}}\,\overline{\mathstrut{\alpha}}+d=0$$ 　再び上の定理，及び補足により $$a\left(\overline{\alpha}\right)^3+b\left(\overline{\alpha}\right)^2+c\overline{\alpha}+d=0$$ 　これは $\overline{\alpha}$ も元の方程式の解であることを意味する．

■

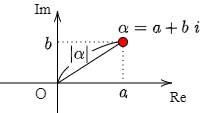
2.4　複素数の絶対値

　複素数 $\alpha=a+b\,i$ に対して，$\sqrt{a^2+b^2}$ を $\alpha$ の絶対値といい，$|\alpha|$ で表す：

$$|\alpha|=|a+bi|=\sqrt{a^2+b^2}$$

　複素平面においては，点A($\alpha)$ の点0からの距離が $|\alpha|$ である．

　ここで， $$\alpha\overline{\alpha}=(a+b\,i)(a-b\,i)=a^2+b^2$$ により次が成り立つ：

重要 $$|\alpha|^2=\alpha\overline{\alpha}$$

重要な補足

　この式は左辺から右辺への書き換えはもちろんのこと，右辺から左辺への書き換えも重要である：

$|\alpha|^2$ を $\alpha\overline{\alpha}$ へと書き換える
$\alpha\overline{\alpha}$ を $|\alpha|^2$ へと書き換える

　この辺りの事情は，ベクトルにおいて $|\overrightarrow{a}|^2=\overrightarrow{a}\cdot\overrightarrow{a}$ という等式で，左辺から右辺への書き換えが，右辺から左辺への書き換えと同等に重要であったことと全く同じである．

　$|\alpha|^2=\alpha\overline{\alpha}$ の書き換えは複素平面のつまずきポイントの1つで，$x$ が実数のとき $|x|^2=x^2$ であったために，複素数 $\alpha$ でも同じように $|\alpha|^2=\alpha^2$ とやってしまうなどのミスが起こりやすい．実際，$\alpha=a+b\,i$ のとき

$$\begin{align*} &|\alpha|^2=(a+b\,i)(a-b\,i)=a^2+b^2\\[5pt] &\ \alpha^2=(a+b\,i)^2=a^2-b^2+2ab\,i \end{align*}$$

であり，両者は一致するとは限らない．また，$\alpha$ が虚数であっても $|\alpha|$ (あるいは $|\alpha|^2$) は必ず実数であるが，$\alpha^2$ の方は実数であるとは限らない．

　「$x$ が実数のとき $|x|^2=x^2$」 に話を戻すと，実は実数も複素数なのだから， 実数 $x$ が $x=a(=a+0\,i)$ だとすれば

$$|x|^2=x\overline{x}=(a+0\,i)(a-0\,i)=a^2=x^2$$

であり，この式の最初と最後を見て $|x|^2=x^2$ と書いていたに過ぎない．同じことだが，2つの複素数 $\alpha,\ \beta$ について

$$|\alpha+\beta|^2=\alpha^2+2\alpha\beta+\beta^2$$

と書いたのでは正しくない．正しくは

$$\begin{align*} |\alpha+\beta|^2&=(\alpha+\beta)\overline{(\alpha+\beta)}\\[5pt] &=(\alpha+\beta)(\overline{\mathstrut{\alpha}}+\overline{\beta})\\[5pt] &=\alpha\,\overline{\mathstrut\alpha}+\alpha\overline{\beta}+\beta\,\overline{\mathstrut\alpha}+\beta\,\overline{\beta}\\[5pt] &=|\alpha|^2+\alpha\overline{\beta}+\overline{\mathstrut\alpha}\beta+|\beta|^2 \end{align*}$$

である．

2.5　2点間の距離

　複素平面上の2点 $\alpha=a+b\,i$，$\beta=c+d\,i$ について，$\beta-\alpha$ の表す点は点 $\alpha$ が原点にくるような平行移動によって点 $\beta$ が移動した点となる．

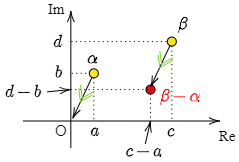
　ここで $\alpha,\ \beta,\ \beta-\alpha$ の表す点をそれぞれA，B，Cとすると，四角形OABCは平行四辺形であるからAB=OC．

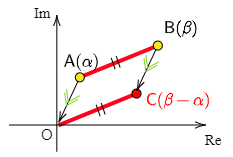
　複素平面において，点Cと原点の距離は複素数 $\beta-\alpha$ の絶対値 $|\beta-\alpha|$ に等しいのであるから2点A($\alpha$)，B($\beta$)間の距離も $|\beta-\alpha|$．

　一般に2つの複素数について，差の絶対値は複素平面上におけるそれら2点間の距離を表す．

$$2\mbox{点}\ \alpha,\ \beta\ \mbox{の距離} :　|\beta -\alpha |$$

補足

　ベクトルでは，${\rm A}(\overrightarrow{\mathstrut a})$，${\rm B}(\overrightarrow{\mathstrut b})$ のとき， $$|\overrightarrow{\rm AB}|=|\overrightarrow{\mathstrut \beta}-\overrightarrow{\mathstrut \alpha}|$$

---

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート	問題
1. 複素平面	[会員]
2. 複素数が表す図形	[会員]
3. 極形式	[会員]		[会員]
4. ド・モアブルの定理	[会員]
5. 複素数と図形	[会員]