高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | [会員] | ||
| 2. 複素数が表す図形 | [会員] | ||
| 3. 極形式 | [会員] | [会員] | |
| 4. ド・モアブルの定理 | [会員] | ||
| 5. 複素数と図形 | [会員] |

1. 複素平面
このノートでは特に断らない限り, などと書けば, は実数であるとする.また, などの文字を断りなく複素数として記述することがある.
1.1 複素(数)平面とは
複素数 ( は実数)について,実部と虚部の組 を座標平面上の点の座標と捉え,複素数 と点 を1対1に対応させる:
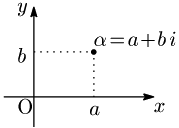
このように平面上の点が1つの複素数を表す平面を複素数平面,又は複素平面(complex plane)という.高校の教科書では「複素数平面」となっているが,大学においては複素平面,複素解析,複素関数など「数」が入らないことが多い.
複素平面の横軸を実軸,縦軸を虚軸という.
複素数 の表す点をAとするとき,この点を A と表す.また,「点 」や「点 」などといった呼び方もする.例えば「点 」や「点 」,「点 」等々.このような呼び方で原点O(オー)は「点 (ゼロ)」である.
実軸上の点はすべて実数であり,逆にすべての実数は漏れなく実軸上にある.また虚軸上の点は を除いてすべて純虚数であり,逆に純虚数はどんなものも虚軸上にある.「数学Ⅱ 複素数と方程式」では実数も複素数の仲間であることを学んだが,複素平面が実軸を含んだものであることから
実数全体の集合は複素数全体の集合の部分集合である
ことが感覚的にも理解し易い.
補足
① このノートでは,複素平面と通常の 平面とを区別するために,両軸を ではなく,Re, Im で表す:
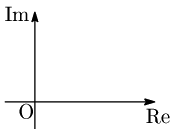
虚軸(Imaginary axis)
② を で表せば,複素数の和と実数倍の定義により, が成り立つ.これはベクトルの成分表示の和,実数倍と完全に同一である.つまり,内積を除くベクトルでの図形的応用は,そのまま複素平面でも使える.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第4章 複素平面
| スライド | ノート | 問題 | |
| 1. 複素平面 | [会員] | ||
| 2. 複素数が表す図形 | [会員] | ||
| 3. 極形式 | [会員] | [会員] | |
| 4. ド・モアブルの定理 | [会員] | ||
| 5. 複素数と図形 | [会員] |