高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | 問題 | |
| 1. 集合 | [無料] | ||
| 2. 場合の数 | [無料] | ||
| 3. 順列 | [会員] | [会員] | |
| 4. 円順列・重複順列 | [会員] | ||
| 5. 組合せ | [会員] | [会員] | |
| 6. 二項定理 | [会員] |

演習問題
問題1【基本】
6人をX,Y,Zの3つのグループに2人ずつ分ける方法は何通りあるか.
問題2【基本】
6人を2人ずつ3つのグループに分ける方法は何通りあるか.
ヒント 問題1との違いに注意が必要です.
問題3【基本】
AからBに最短で行く方法は何通りあるか.
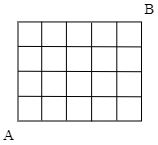
ヒント 計算一発で求める方法とコツコツ書き込む方法があります.
問題4【標準】
は0以上の整数とする. となる の組は何通りあるか.
ヒント 計算一発で求める上手い方法があります.
問題5【標準】
は整数とする.,,, となる の組は何通りあるか.
ヒント 問題4に制限が付きましたが,ちょっと工夫するだけで問題4と同じ設定に帰着できます.
問題6【標準】
は整数とする. となる の組は何通りあるか.
ヒント には大小関係があるので順列の問題かと思いきや,実は組合せの問題です.
問題7【発展】
は整数とする. となる の組は何通りあるか.
ヒント 問題6との違いに注意してください.ちょっとした工夫で計算一発で解決です.
問題8【発展】
は自然数とする. となる の組は何通りあるか.
ヒント 計算一発で解決する工夫を考えてみてください.
問題9【発展】
は0以上の整数とする.,,, となる の組は何通りあるか.
ヒント 「以下」は「以上」よりずっと状況が複雑です.でも発想の転換で実はこれも問題4と同じ設定に帰着できます.

X,Y,Zのどのグループから決めても問題はありません.
解答
Xの選び方が
(通り)
その各々に対してYの選び方が
(通り)
残りは自動的にZとなるから求める総数は
(通り)
今度はX,Y,Zの区別がありません.区別がない場合でも,まずは区別した場合を計算したのち,重複している回数で割ります.
解答
6人をA,B,C,D,E,Fとする.前問の結果から3つのグループをX,Y,Zと区別すると90通り.
このうち例えばAB,CD,EFの組に対してグループ名が
XYZ,XZY,YXZ,YZX,ZXY,ZYX
の6()通りの重複があるから,求める組合せの個数は
(通り)
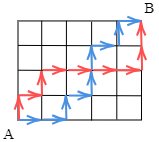
例えば最短経路として上の図のような赤色の経路と青色の経路がありますが,これらの経路を
↑→↑→→→→↑↑
→→↑→↑↑→↑→
と表現すると,
最短経路と「→5本と↑4本の順列」が1対1に対応する
ということがわかります.このように順列・組合せでは対象そのものではなく,それらと1対1に対応する別のもので,順列・組合せの総数を数えやすいものを考えるということが非常にしばしば行われます.
解答
題意の最短経路は「→5本と↑4本の順列」と1対1に対応する.↑の位置を決めると残りの位置は自動的に→となるから,求める最短経路の総数は
(通り)
別解 [数値記入法]
こういった格子状の最短経路問題では,次のように数値を順に書き込んで足していくと答えが得られます.
