高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | 問題 | |
| 1. 集合 | [無料] | ||
| 2. 場合の数 | [無料] | ||
| 3. 順列 | [会員] | [会員] | |
| 4. 円順列・重複順列 | [会員] | ||
| 5. 組合せ | [会員] | [会員] | |
| 6. 二項定理 | [会員] |

5.組合せ
5.1 組合せ
数学における「組合せ」とは
a,b,c の3文字から2文字を選んで一列に並べる順列は,
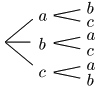
の6通りがある.このうち
ab と ba,bc と cb,ca と ac
は選んだ文字がそれぞれ同じになっている.選んだ2つを一列に並べたりしないで,どの2つが選ばれたかだけに興味をもつならこのような重複を考慮して
{a,b},{b,c},{c,a}
の3組だけとなる.この各組を,異なる3個のものから2個を選ぶ組合せといい,その総数を
3C2
で記号化する.すなわち 3C2=3 である.
組合せと順列の関係
順列 3P2 との関係は,上の各組において順番まで考慮したものが順列であり,この場合だと各組合せから 2!=2×1=2(通り)の順列ができるから,
3C2×2!=3P2∴ 3C2=3P22!(=3⋅22⋅1=3)
一般に異なる n 個のものから r 個選ぶ組合せは,
nCr=nPrr! (通り)
である.更に,nPr=n!(n−r)! であったから,
nCr=n!(n−r)!r!
とも書ける.
また,nC0=1 と定める.
補足
「C」は英語で組合せを意味する ‘Combination’ の頭文字である.
組合せ 異なる n 個のものから r 個選ぶ組合せの総数は,nCr=nPrr!=n!(n−r)!r! 特にnC0=1

5.2 組合せの種々の公式
nCr を使ったいくつかの公式
nCr を使ったいくつかの公式を確認しておこう.
[1] nCr=nCn−r[2] nCr=n−1Cr−1+n−1Cr[3] rnCr=nn−1Cr−1
[1]は利用頻度が高く,例えば 9C7 などを計算したいときに大いに助かる.[2]と[3]はやや程度が高い.
証明
[1] (左辺) =n!(n−r)!r!
(右辺) =n!{n−(n−r)}!(n−r)!=n!r!(n−r)!
よって,(左辺) = (右辺)
[2] (右辺)=(n−1)!{(n−1)−(r−1)}!(r−1)!+(n−1)!{(n−1)−r}!r!=(n−1)!(n−r)!(r−1)!+(n−1)!(n−r−1)!r!=(n−1)!{r+(n−r)}(n−r)!r! (←通分して計算)=(n−1)!×n(n−r)!r!=n!(n−r)!r!=(左辺)
[3] (左辺)=r⋅n!(n−r)!r!=n⋅(n−1)!(n−r)!(r−1)!=n⋅(n−1)!{(n−1)−(r−1)}!(r−1)!=(右辺)
■
補足
次のように考えれば納得しやすい上に記憶もしやすい
上の性質は,次のように考えると理解しやすい.
[1] n 人から r 人の掃除当番を決めるのに,掃除当番でない n−r 人を決めれば,残りが自動的に掃除当番となる.
[2] パスカルの三角形
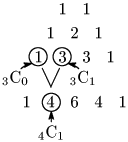
4C1=3C0+3C1
[3]
rnCr:n 人から r 人のグループを作り,更にその中からボスを選ぶ.
nn−1Cr−1:まずボスを決めて,残りの n−1 人からグループに入る r−1 人を選ぶ.

5.3 同じものを含む順列
n 個の中に同じものがいくつか含まれる場合
nCr は n 個がすべて異なっていることが前提であるので,n 個の中に同じものが含まれている場合は注意が必要である.
例題 1,1,2の3つの数を使って3桁の数は何通りできるか.
2つある1を,1a,1b と区別する:
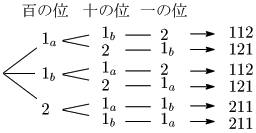
全6通りのうち,2つ(=2!) ずつ同じものがあるから,
3!2!=3⋅2⋅12⋅1=3 通り
n 個のうち,p 個の同じもの,q 個の同じもの,r 個の同じものがあり,これらを1列に並べる場合が何通りあるかを考える.まずはどんなに同じに見えるものでも区別して順列を考えると n! 通り.このうち,p! 通りの区別のできないものが含まれる,即ち n! 通りの中には p! 重カウントされているものがあるから p! で割る.同様に q! 重カウント,r! 重カウントになっているものがあるからそれらを割る.
一般に次が成り立つ:
同じものを含む順列 n 個のうち,p 個の同じもの,q 個の同じもの,r 個の同じものがるとき,これらを1列に並べる方法は,n!p!q!r! 通り

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | 問題 | |
| 1. 集合 | [無料] | ||
| 2. 場合の数 | [無料] | ||
| 3. 順列 | [会員] | [会員] | |
| 4. 円順列・重複順列 | [会員] | ||
| 5. 組合せ | [会員] | [会員] | |
| 6. 二項定理 | [会員] |