4. 円順列・重複順列(ノート)
スライドで学ぶ高校数学

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学A　第1章　場合の数

4．円順列・重複順列

例題　A,B,C,Dの4人が円形に座る方法は何通りあるか．

　円順列では，回転すると同じなるものは区別しない．従って次の4通りは，同じものとして区別しない：

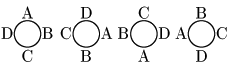
　すると順列を考えるとき，同じものでないかどうかをいちいち回転させてチェックしなければならず，わずらわしい．そこで次の考え方がポイントとなる：

ポイント誰か1人を固定する．

　例えばAの座席を固定してしまうと，残り3人の座り方(順列)を考えればよいから，

$(4-1)\,!=3\,!=3\times2\times1=6$ (通り)

※ スライド (会員向け)に詳しい解説あり．

　一般に次が成り立つ：

　異なる $n$ 個のものを円形に並べる方法は $(n-1)\,!\ \mbox{通り}$

　円順列の考え方にはもう一つ強力なものが存在する．特に同じものを含む円順列を考える際には，上で見た固定して考えるのに比べて処理時間は雲泥の差となる．詳しくは，高校数学ワンポイント同じものを含む円順列 を参照．

例題　A,B,C,Dの異なる4つの石でネックレスを作る方法は何通りあるか．

　数珠やネックレスといった持ち上げられるものは，回転させて同じになるものを区別しないのはもちろんのこと，ひっくり返して同じになるものも区別しない：

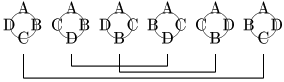
　すべて異なる石の場合，必ず2つずつのペアが存在するから，求めるものは円順列の総数の半分になる：

$\dfrac{(4-1)!}2=3$ (通り)

　一般に次が成り立つ：

　異なる $n$ 個の石を用いてネックレスを作る方法は $\frac{(n-1)\,!}2\ \mbox{通り}$

例題　1,2,3の3つの数を繰り返し用いることを許してできる2桁の数は何通りあるか．

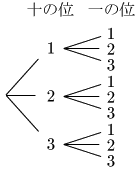
　樹形図より，最初の枝が3本，その各枝からそれぞれ3本ずつ枝が出ているから，

$3\times3=3^2=9$ (通り)

　一般に次が成り立つ：

異なる $n$ 個から重複を許して $r$ 個び，一列に並べる方法は

$n^r$ 通り

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

数学A　第1章　場合の数