高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | 演習 | |
| 1. 集合 | [無料] | ||
| 2. 場合の数 | [無料] | ||
| 3. 順列 | [会員] | [会員] | |
| 4. 円順列・重複順列 | [会員] | ||
| 5. 組合せ | [会員] | [会員] | |
| 6. 二項定理 | [会員] |
1．集合
1.1 集合
物の集まりを集合という．日常生活でも「集合」という言葉は用いられているので数学における「集合」との違いを述べておきたい．
数学では属するか属さないかが明確に区別できるものの集まりが集合である．例えば「さいころの目の数の集まり」を考えると，1から6の整数ならばその集合に属するがそれ以外の数は属さないとはっきり区別できるから集合といえる．一方，「安いスーパーの集まり」を考えると，1つのスーパーをとってみても，ある人は安いと言うし，また別の人は安くないと言うなど答えがまちまちであることが起こり得る．これは「安いスーパー」の定義が明確でないためで，「安いスーパーの集まり」というだけでは数学における集合にはならない．
集合の表し方
さいころの目の集合を考えると，そこに属するのは1, 2, 3, 4, 5, 6 の6つの数である．この集合を $A$ と名付けたとき，集合 $A$ を次のように書き表す：
\[A=\{1,\ 2,\ 3,\ 4,\ 5,\ 6\}\]
このとき小カッコ( )ではなく中カッコ{ }を用いていることに注意する．
集合に含まれる1つ1つの数を，その集合の要素または元(げん)という．
ある数 $x$ が集合 $A$ の要素であることを
\[x\in A\]
と書き表す．この場合，
\[1\in A,\ 2\in A,\ \cdots,6\in A\]
である．一方，ある数 $y$ が集合 $A$ の要素でない場合は
\[y\not\in A\]
で書き表す．例えば，
\[7\not\in A,\ \frac12\not\in A,\ -5\not\in A\]
など．
集合 $A$ の個数を $n(A)$ で書き表す：
\[n(A)=6\]
集合の様々な表し方
集合は，さいころの目の数のように要素が有限個しかない有限集合と，要素が無限個ある無限集合の2つに大別される．有限集合の場合はこれまで書いてきたように中カッコでくくって要素をその中に書き尽くす（列挙する）という形で表すことができるが，無限集合だとそうもいかない．そこで集合を表す別な方法として条件を指定する方法がある．
列挙 ：$A=\{1,2,3,4,5,6\}$
条件指定：$A=\{n\ |\ 1\leqq n\leqq 6,n$ は整数}
(バー‘｜’の右に条件をかく．)
$B=\{2n\ |\ n$ は整数}
→ $B$ は偶数全体の集合
$C=\{x\ |\ -1\leqq x<2\}$
→ $C$ は $-1$ 以上2未満の実数の集合
1.2 部分集合
ある集合 $U$ の要素の一部分の集まりを，その集合 $A$ の部分集合という．気を付けなければならないのは，「部分」と言っておきながら集合 $U$ そのものも $U$ の部分集合であることと，のちに学習する空集合 $\varnothing$ も集合 $U$ の部分集合であるということの2点である．前者については部分集合の数学的な定義を見ると理解しやすい．
部分集合の定義
集合 $A$ が集合 $U$ の部分集合であるとは，$A$ のどんな要素も $U$ の要素であるときをいう：
$A$ が $U$ の部分集合
$\iff$ 常に「$a\in A \Longrightarrow a\in U$」が成り立つ．
$A$ も $U$ に置き換えると
常に「$a\in U \Longrightarrow a\in U$」が成り立つ．
となるが，これはいかにも当たり前のことである．従って $U$ 自身も $U$ の部分集合であることがわかる．
例
$A=\{1,\ 3,\ 6\}$
$B=\{1,\ 2,\ 3,\ 4,\ 5,\ 6\}$
このとき $A$ は $B$ の部分集合である．
集合 $A$ が集合 $B$ の部分集合であるとき，
$A\subset B$ (または $B\supset A$)
と表す：
$A\subset B\iff A$ のどの要素も $B$ の要素
また，2つの集合 $A$，$B$ の要素が完全に一致しているとき，すなわち $A\subset B$ かつ $A\supset B$ のとき，$A=B$ で表す：
$A=B\iff A\subset B$ かつ $A\supset B$
問題で「2つの集合 $A,B$ について $A=B$ を示せ」というのがあったら，それは「$A\subset B$ と $A\supset B$ の2つを示せ」という意味である．
1.3 共通部分と和集合
2つの集合 $A,B$ の両方に属している要素の集合を，$A$ と $B$ の共通部分といい，$A\cap B$ で表す．読み方は
- $A$ と $B$ の共通部分
- $A$ キャップ $B$（$\cap$ の形がキャップ(野球帽)に似ている）
- $A$ と $B$ のインターセクション(intersection)
など．
また，$A$ と $B$ の少なくとも一方に属する要素の集合を $A$ と $B$ の和集合といい，$A\cup B$ で表す．読み方は
- $A$ と $B$ の和集合
- $A$ カップ $B$（$\cup$ の形がコーヒーカップに似ている）
- $A$ と $B$ のユニオン(union)
など．
例 $A=\{1,2,4,5\}$，$B=\{2,3,4\}$
$A$ と $B$ の共通部分：$A\cap B=\{2,4\}$
$A$ と $B$ の和集合 ：$A\cup B=\{1,2,3,4,5\}$
要素の個数の公式
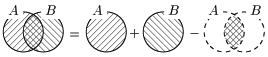
2つの集合 $A,B$ について，$A\cup B$ の要素の個数を考えよう．$A\cap B=\varnothing$ すなわち2つの集合に共通な要素がない場合は，$A$ と $B$ のそれぞれの要素の個数を足すだけでよい．一方，$A\cap B\neq\varnothing$ すなわち2つの集合に共通な要素がある場合は，$A$ と $B$ のそれぞれの要素の単純に個数を足したのではダブルカウントが生じてしまう．従って $A\cup B$ の要素の個数は次のように計算される：
2集合の公式 \[n(A\cup B)=n(A)+n(B)-n(A\cap B)\]
補足
$A\cap B=\varnothing$ の場合，$n(A\cap B)=0$ となるため上の公式はこの場合も含んでいる．
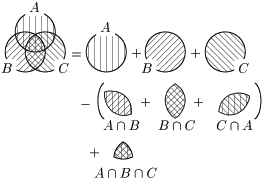
2つの集合の場合と同様に，3つの集合の場合も，ダブルカウント，トリプルカウントを解消するように次のように計算される：
1.4 いろいろな集合
空集合
- 要素が全くない集合．
- $\varnothing$ または $\emptyset$ で表す．
(ギリシャ文字の $\phi$ (ファイ)は形こそ似ているが全く関係がないのでこれらの記号をファイと読むべきでない．) - $\varnothing$ も集合の1つで，すべての集合の部分集合であると考える．
補集合
例
全体集合 $U=\{1,\ 2,\ 3,\ 4,\ 5,\ 6\}$
$A=\{2,\ 4,\ 6\}$
全体集合 $U$ の要素で，$A$ に属さない要素の集まりを$A$ の補集合といい，$\overline{A}$ で表す．上の例では
$\overline{A}=\{1,\ 3,\ 5\}$
補足
「集合 $A$ の補集合」の補集合は，元の集合 $A$ である：
$\overline{\overline{A}}=A$
例題 集合 $U=\{a,b,c\}$ の部分集合をすべて列挙せよ．
答
解答例を表示する1.5 ド・モルガンの法則
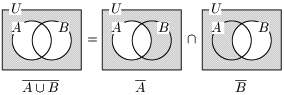
$A,B$ を集合とする．和集合 $A\cup B$ の補集合 $\overline{A\cup B}$ と，共通部分 $A\cap B$ の補集合 $\overline{A\cap B}$ について，それぞれ以下に示すような関係が成り立ち，これら2つの関係式をあわせてド・モルガンの法則(De Morgan’s laws)という．
ド・モルガンの法則1 \[\overline{A\cup B}=\overline{A}\cap\overline{B}\]
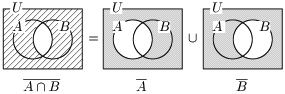
ド・モルガンの法則2 \[\overline{A\cap B}=\overline{A}\cup\overline{B}\]
補足
ド・モルガン(Augustus de Morgan, 1806-1871)はイギリスの数学者である．高校数学では名前がよく似ている「ド・モアブルの定理」というものもある．詳しくは数学Ⅲ 第4章複素平面 ド・モアブルの定理 を参照．
このページで疑問は解決されましたか？
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第1章 場合の数
| スライド | ノート | 演習 | |
| 1. 集合 | [無料] | ||
| 2. 場合の数 | [無料] | ||
| 3. 順列 | [会員] | [会員] | |
| 4. 円順列・重複順列 | [会員] | ||
| 5. 組合せ | [会員] | [会員] | |
| 6. 二項定理 | [会員] |