中学1年数学 第1章 正の数と負の数
1.1 正の数と負の数
1.2 加法と減法
1.3 加法の計算法則
1.4 乗法と除法
1.5 乗法の計算法則
1.6 四則の混じった計算
5.1 逆数
6÷2＝3ですが，$6\times\dfrac12$ も3です。
6÷(－2)＝－3ですが，$6\times\left(-\dfrac12\right)$ も－3です。
(－6)÷2＝－3ですが，$(-6)\times\dfrac12$ も－3です。
(－6)÷(－2)＝3ですが，$(-6)\times\left(-\dfrac12\right)$ も3です。
これら4つの例で主張したいことは
除法は乗法に書き換えることができる
ということです。上の計算例では
(ある数)÷2 → (ある数)×$\dfrac12$
(ある数)÷(－2) → (ある数)×$\left(-\dfrac12\right)$
となっていますが，「÷2」が「×$\dfrac12$」になり，「÷(－2)」が「×$\left(-\dfrac12\right)$」に変化しています。2と$\dfrac12$，－2と $-\dfrac12$ はそれぞれどのような関係でしょうか？
答えは
2つの数を掛けると1になる
という関係です。実際，$2\times\dfrac12=1$ であり， $(-2)\times\left(-\dfrac12\right)=1$ となっています。
このように，掛けると1になる2数は互いに逆数(ぎゃくすう)の関係であるといいます。2の逆数は $\dfrac12$ です。$\dfrac12$ の逆数は2です。同様にして，－2の逆数は $-\dfrac12$ で，$-\dfrac12$ の逆数は－2です。
逆数$A$ の逆数は $\dfrac1A$，$\dfrac1A$ の逆数は $A$
注意
0以外の数はどんな数にも逆数があります。0には逆数がありません。0×□＝1となる□がないからです。
逆数を用いると，除法は乗法に書き換えることができる
小学校の時に，例えば3÷4は $\dfrac34$ に等しいということを学びました。$\dfrac34$ は $3\times\dfrac14$ と書き換えることができます。よって
\[3\div4\left(=\dfrac34\right)=3\times\dfrac14\]
という関係が成り立ちます。このように除法の記号「÷」を，乗法の記号「×」に書き換えることができるのです。このとき4が $\dfrac14$ に変化しましたが，4と $\dfrac14$ は積が1となりますから逆数の関係にあります。つまり
ある数 $A$ で割ることと，その逆数である $\dfrac1A$ を掛けることは同じである
ということがいえます。
例題 次の除法の式を，乗法になおして計算しなさい。
(1) $3\div(-4)$
(2) $(-5)\div3$
(3) $\dfrac12\div\dfrac16$
(4) $\left(-\dfrac49\right)\div\left(-\dfrac23\right)$
こたえ
(1) $3\div(-4)=3\times\left(-\dfrac14\right)=-\dfrac34(=-0.75)$
(2) $(-5)\div3=(-5)\times\dfrac13=-\dfrac53$
(3) $\dfrac12\div\dfrac16=\dfrac12\times6=3$
(4) $\left(-\dfrac49\right)\div\left(-\dfrac23\right)=\left(-\dfrac49\right)\times\left(-\dfrac32\right)=\dfrac23$
5.2 乗法の性質
乗法の交換法則と結合法則
加法では次の交換法則と結合法則が成り立ちました。
加法の計算法則 [1] 加法の交換法則 $a+b=b+a$
[2] 加法の結合法則 $(a+b)+c=a+(b+c)$
乗法においても，
2×3＝3×2 【交換法則】
(2×3)×4＝2×(3×4) 【結合法則】
といったように，交換法則と結合法則が成り立ちます。
乗法の計算法則 [1] 乗法の交換法則 $a\times b=b\times a$
[2] 乗法の結合法則 $(a\times b)\times c=a\times (b\times c)$
例題1 次の計算をしなさい。
(－4)×3.14×(－2.5)
こたえ
(－4)×3.14×(－2.5)
＝3.14×(－4)×(－2.5) 【交換法則】
＝3.14× {(－4)×(－2.5)} 【結合法則】
＝3.14×10
＝31.4
答えは 31.4
除法では交換法則や結合法則が成り立たない
$2\div5=\dfrac25(=0.4)$ で，$5\div2=\dfrac52(=2.5)$ となりますから除法では交換法則が成り立ちません。また，$(8\div4)\div2=1$ で，$8\div(4\div2)=4$ となりますから除法では結合法則も成り立ちません。しかし，逆数を使えば除法は乗法に書き換えることができました。このことにより，除法においても交換法則や結合法則を利用することができるようになるのです。除法の計算ではいつでも乗法に書き換える癖をつけておくのがよいでしょう。
ポイント除法は乗法に書き換えておくのが基本
例題 次の計算をしなさい。
$36\div(-15)\div18$
こたえ
$36\div(-15)\div18$
=$36\times\left(-\dfrac1{15}\right)\times\dfrac1{18}$ （すべて乗法で表す)
=$\left(-\dfrac1{15}\right)\times36\times\dfrac1{18}$ 【交換法則】
=$\left(-\dfrac1{15}\right)\times\left(36\times\dfrac1{18}\right)$ 【結合法則】
=$\left(-\dfrac1{15}\right)\times2$
＝$-\dfrac2{15}$
答えは $-\dfrac2{15}$
積の符号と絶対値
正の数だけの乗法と，負の数を含んだ乗法との違いを確認していきましょう。例えばー2を何個も掛けていくとどうなるでしょうか。
－2
(－2)×(－2)＝4
(－2)×(－2)×(－2)＝－8
(－2)×(－2)×(－2)×(－2)＝16
(－2)×(－2)×(－2)×(－2)×(－2)＝－32
この結果から，負の数を含んだ乗法の積の符号と絶対値は次のようなっていることがわかります。
例題 次の計算をしなさい。
$(-4)\times5\times\left(-\dfrac13\right)\times(-6)$
こたえ
積の符号 負の数が3個(奇数)あるから －
積の絶対値 $|-4|\times|5|\times\left|-\dfrac13\right|\times|-6|=40$
答えは －40
5.3 累乗
例えば，2×2×2のように同じ数を複数個掛けるとき，3個くらいならまだしも
2×2×2×2×2×2×2×2×2×2×2×2×2
になると，2が何個掛けられているかがとてもわかりにくいです。こんな時，数学には便利な表現方法があります。例えば上の式は，2が13個掛けられているのですが，これを $2^{13}$ というように表現するのです。読み方は「2の13乗」です。
一般に，ある数 $a$ を $n$ 個掛けるとき，これを $a^n$ と表現し，「$a$ の $n$ 乗」と読みます。また $n$ を指数(しすう)といいます。そして，$a^2$，$a^3$，$a^4$，… をまとめて $a$ の累乗(るいじょう)といいます。
$a$ の累乗
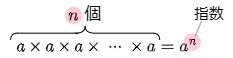
累乗表現における注意事項
累乗の表現ではカッコ( )を付ける，付けないでは結果が異なる場合がありますから注意しなければなりません。次の例で確認しておきましょう。
例1 $(-3)^2=(-3)\times(-3)=9$
$-3^2=-(3\times3)=-9$
例2 $\left(\dfrac32\right)^2=\dfrac32\times\dfrac32=\dfrac94$
$\dfrac32^2=\dfrac{3\times3}2=\dfrac92$
問題1 次の逆数を求めなさい。
(1) $\dfrac73$ (2) $-\dfrac67$ (3) $-\dfrac18$
(4) $5$ (5) $1$ (6) $-1$
ヒント 掛けて1になる数が，その数の逆数です。
こたえ
問題2 次の計算をしなさい。
(1) $\dfrac65\div(-3)$ (2) $\left(-\dfrac5{12}\right)\div\dfrac{10}9$ (3) $-\dfrac{15}{32}\div\left(-\dfrac38\right)$
ヒント すべて乗法に書き換えてから計算します。
こたえ