4．乗法と除法

中学1年数学　第1章　正の数と負の数

1.1　正の数と負の数
1.2　加法と減法
1.3　加法の計算法則
1.4　乗法と除法
1.5　乗法と除法の性質

4.0 はじめに

　小学校では何か新しい計算が登場すると，必ず具体例を考えながら理解してきました。2×3ですと，例えば「あめを1人に2個ずつ配ります。3人に配るとき，あめは何個必要ですか」といった問題を考えることで理解しようという訳です。これから負の数を含む掛け算や割り算を学習していきますが，掛け算の方はこれまで通り具体例で考えることができても，割り算の方はそれが大変に難しくなります。中学校以降の数学においては，

具体的なものから抽象的なものへ

という流れが強くなっていきます。この思考の転換になじめないと，中学校以降の数学でつまずく原因となります。無理のある具体例で覚えようとするよりはむしろ，そういうルールだと思って受け入れる方が良いように思います。

　例えば，負の数どうしを掛けると正の数になるということを，このあとすぐに学習します。でも(負の数)×(負の数)がどうして正の数になるのでしょう？中学校の数学でつまずく最初の1歩がここになる人は多いはずです。こういった計算を具体例で考えることはできます。実際，以下でも2つの例を挙げています。しかし説明している筆者ですら「これってわかりやすい例なのかなあ」と実は思ったりもしています。それならいっそのこと「掛け算とは数直線を用いたルールによって決められる計算のこと」と割り切った方が，あとあと良いのではないかと思いました。従いまして，以下では掛け算とはどのような計算を指すのかを，まずは数直線を用いて説明しています。

4.1 乗法

　掛け算のことを乗法(じょうほう)といいます。例えば2×3という乗法の答えは6ですが，6をこの乗法の積(せき)といいます。乗法について，まずは数直線を用いて説明していきましょう。

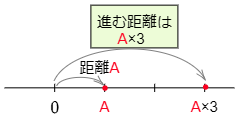
●正の数をかける

　例えば，ある数Aに3を掛ける計算であるA×3の場合，数直線を用いて次のように計算します。

例1　(－2)×3

　数直線上で原点から－2までは，距離が2で左向き。
→左向きに，原点からの距離が2×3のところまで進む。
→その点が表す数である―6が答えとなる。

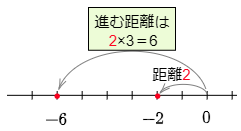
答えは　－6

例2　(－2)×0.5

　数直線上で原点から－2までは，距離が2で左向き。
→左向きに，原点からの距離が2×0.5のところまで進む。
→その点が表す数である－1が答えとなる。

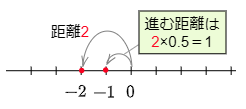
答えは　－1

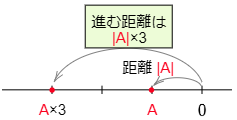
●負の数を掛ける

　例えば，ある数Aに－3を掛ける計算であるA×(－3)の場合，数直線を用いて次のように計算します。

　このように，負の数を掛けるということは，加法や減法のときがそうであったように，向きが逆転すると理解しておくと間違いがありません。

ポイント負の数を掛ける　→　進む向きが逆転

例3　2×(－3)

　数直線上で原点から2までは，距離が2で右向き。
→逆の左向きに，原点からの距離が2×3のところまで進む。
→その点が表す数である－6が答えとなる。

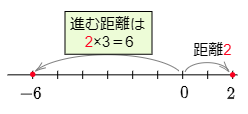
答えは　－6

例4　(－2)×(－3)

　数直線上で原点からの－2までは，距離が2で左向き。
→逆の右向きに，原点からの距離が2×3のところまで進む。
→その点が表す数である6が答えとなる。

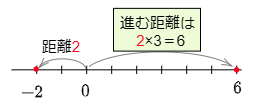
答えは　6

4.2 除法

　割り算のことを除法(じょほう)といいます。例えば6÷2の答えは3ですが，3をこの除法の商(しょう)といいます。除法を負の数にまで拡張しようとするとき，何か具体例で理解しようとすると，これがなかなか難しいのです。例えば，6÷(－2)という除法を何かに例えて理解しようとすると，どうしても「－2等分する」という部分を他の表現に置き換えることが困難です。そこで，負の数の除法を理解するには，除法そのものの意味を変更しなければなりません。

除法の意味とは

　6÷2の答えは3です。つまり6÷2＝3です。このとき，6＝2×3が成り立ちます。逆に6＝2×3が成り立つとき，6÷2＝3が成り立ちます。

6÷2＝3　$\iff$　6＝2×3

　この関係を利用して

割り算とは，掛け算から考えるもの

というように考え方を転換するのです。つまり6÷2＝□で，□の値が知りたいと思ったら，掛け算になおして6＝2×□と表し，□にあてはまる数を考えるのです。

※この考え方は，高校生になったとき，文字式を文字式で割るというところでも生きてきます。意欲的な方はこちら をどうぞ。

ポイント除法は乗法から

●正の数で割る

例1　(－6)÷2

(－6)÷2の答えを□とすると
　(－6)÷2＝□　→　－6＝2×□
よって　□＝－3

答えは　－3

例2　(－6)÷0.5

(－6)÷0.5の答えを□とすると
　(－6)÷0.5＝□　→　－6＝0.5×□
よって　□＝－12

答えは　－12

●負の数で割る

例3　6÷(－2)

6÷(－2)の答えを□とすると
　6÷(－2)＝□　→　6＝－2×□
よって　□＝－3

答えは　－3

例4　6÷(－0.5)

6÷(－0.5)の答えを□とすると
　6÷(－0.5)＝□　→　6＝(－0.5)×□
よって　□＝－12

答えは　－12

例5　(－6)÷(－2)

(－6)÷(－2)の答えを□とすると
　(－6)÷(－2)＝□　→　－6＝(－2)×□
よって　□＝3

答えは　3

0を含む除法の考え方

● 0を割る

　0÷2の答えが□だとすると，
　　0÷2＝□　→　0＝2×□
　よって　□＝0

　このように0を，0でない数 $a$ で割ると，$0=a\times\square$ から□は常に0となります。

● 0で割る

　2÷0の答えが□だとすると，
　　2÷0＝□　→　2＝0×□
　この□に当てはまる数はありません。0にどんな数を掛けても0になり，決して2になることはありません。

まとめ・0÷(0でない数)＝0
・どんな数も「0で割る」ことはできない

問題1　次の計算をしなさい。
(1)　(＋5)×(＋4)
(2)　(＋3)×(－3)
(3)　(－8)×7
(4)　(－10)×(－6)

問題2　次の計算をしなさい。
(1)　(＋12)÷(＋4)
(2)　(＋8)÷(－2)
(3)　(－14)÷7
(4)　(－20)÷(－5)