中学1年数学 第1章 正の数と負の数
1.1 正の数と負の数
1.2 加法と減法
1.3 加法の計算法則
1.4 乗法と除法
1.5 乗法と除法の性質

3.1 加法の計算法則
例えば,2+3と3+2はともに5になります。(-2)+3と3+(-2)はともに1になります。このように加法,すなわち足し算では,計算の順番を変えても答えが同じになります。この計算の順番を交換できる決まりを加法の交換法則(こうかんほうそく)といいます。
また,(2+3)+4と2+(3+4)はともに9になります。 と はともに-5になります。このように加法では計算の優先順位を変更しても答えが同じになります。この計算の優先順位を変更できる決まりを加法の結合法則(けつごうほうそく)といいます。
加法の計算法則 [1] 加法の交換法則
[2] 加法の結合法則
減法には交換法則や結合法則はないの?
例えば,2-3はー1,3-2は1ですから,減法,すなわち引き算では交換法則が成り立ちません。
また, は-5で, は3ですから,減法では結合法則も成り立ちません。
これで減法では交換法則も結合法則も成り立たないことがわかりました。ところが,ちょっと工夫すると,減法もある種の交換法則や結合法則を成り立たせることができます。その工夫とは?
減法を加法に書きかえる
例えば,2-3という計算は数直線上において,2から左向きに3だけ進んだ点が表す-1となります。この左向きというのが減法の記号「-」からきていた訳ですが,これを右向き進めを意味する加法の記号「+」に変えることができます。それには「左向きに3だけ進む」を「右向きに―3だけ進む」としてやればよいのです。
2-3 → 2+(-3)
もう1つ例を見ておきましょう。 は数直線上の2から左向きに-3だけ進むことを意味し,これを右向きに3だけ進むと言い換えるのでした。
2-(-3) → 2+(+3)
このように,減法の記号「-」を加法の記号「+」に変更する代わりに,記号のすぐ後ろの数の符号をひっくり返すことで,どんな減法も加法によって表すことができるのです。

3.2 加法と減法の混じった式
前の節で,加法はもちろん,減法も加法に書き換えることで交換法則や結合法則が使えることを学びました。これらの法則を上手に利用して計算の工夫をしてみましょう。
例題 17-58+23-62
こたえ
考え方① 前から順番に計算する
17-58=-41
-41+23=-18
-18-62=-80
答えは -80
考え方② 交換法則や結合法則を利用
まずはすべて加法で表します。
17-58+23-62
=(+17)+(-58)+(+23)+(-62)
これで,どの数も自由に交換できるようになりましたから,加法の交換法則を使って計算の工夫を考えます。中央の2つを入れ替えると良さそうです。
(+17)+(-58)+(+23)+(-62)
=(+17)+(+23)+(-58)+(-62)
更に,加法の結合法則を使って前2つと,後ろ2つをそれぞれ計算します。
{(+17)+(+23)}+{(-58)+(-62)}
あとはこれを計算して
(+40)+(-120)=40-120=-80
答えは -80
「項」という用語と,加法の記号の省略
先ほどの例題で,考え方②では最初にすべて加法に変換しましたが,正の数にも符号がついていました。「正の符号の+は省略できたはずなのにどうして?」そんな風に思いませんでしたか?
17-58+23-62
→ (+17)+(-58)+(+23)+(-62)
この点について詳しくお話していきましょう。

式全体を加法で表したとき,+17,-58,+23,-62の4つの数を,この式の項(こう)といいます。正の数である+17と+23を正の項,負の数である―58と-62を負の項といいます。この式には正の項と負の項を合わせて4つの項がありますから「項数は4である」という言い方もされます。17-58+23-62というのはこの4つの項の和である(+17)+(-58)+(+23)+(-62)の加法の記号「+」を省略したものだと考えるのです。
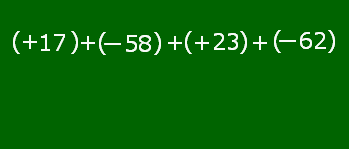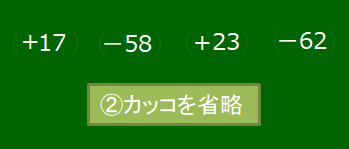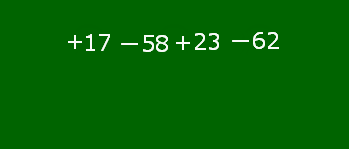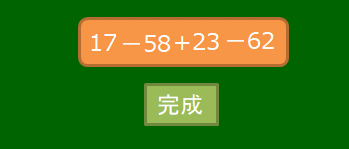
17-58+23-62ができるまで
よって,式全体を加法に変換するにはこの逆の操作をしてやります。
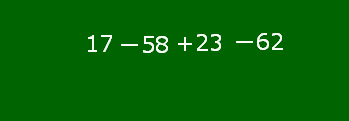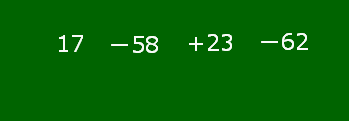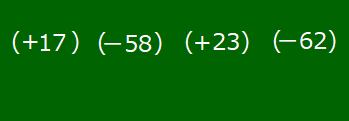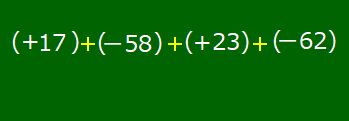
このように複数の項からなる式において,符号は原則として省略できません。省略できるのは加法の記号「+」の方なのです。例外として,+17のように式の先頭が正の数の場合のみ,+記号を省略できます。
加法の交換法則と結合法則を,この「項」という用語を用いて説明すると次のようになります。
加法においてはどの2つの項も交換可能で,どの2つの項とも結合可能である。
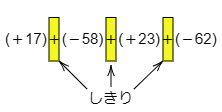
「+」という記号には加法の意味と,正の符号の意味の2つがあることは前節のコラム で述べました。加法の記号+は式を項に分けるしきりの役割を果たしているのです。

演習1 次の計算をしなさい。
(1) 5-8+13-2
(2) -4+15+3-16
(3) 10+(-3)-(-6)
(4) 8.1-3.4-(-1.7)
(5)
(6)
こたえ
