2．加法と減法

中学1年数学　第1章　正の数と負の数

1.1　正の数と負の数
1.2　加法と減法
1.3　加法の計算法則
1.4　乗法と除法
1.5　乗法と除法の性質

　この節のタイトルである加法と減法は，やさしい言葉で言うと足し算と引き算です。振り返ってみると，足し算と引き算はなんと小学校1年生の時から習っています。こういった計算は生活していく上でも必要となるため，小さいうちから学ばせているのですね。

　さて，前節で数の世界を負の数にまで拡張しましたから，これらの数も含めた足し算，引き算を見ていきましょう。

2.1 加法

　足し算のことを加法(かほう)といいます。例えば1＋2のような計算です。加法の計算結果を和(わ)といいます。１＋2の場合，和は3です。0以上の数どうしを足す計算は小学校で学習済みですから，ここでの話題は専ら負の数を含んだ足し算です。

　さて，負の数を交えた足し算を理解するスペシャルなアイデアを紹介します。それは数直線を用いることです。数直線を用いることで，加法を目で捉えるのです。

　加法は「＋」を用いて1＋２のようにA＋Bの形をしています。このA＋Bの「＋」は，数直線上を「右向きに進め」の意味となります。

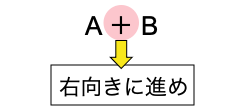
　このとき，加法は数直線を用いて次のように計算します。

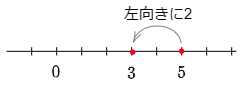
例1　5＋(－2)

　　数直線上の5をとる
→　そこから右向きに－2進む
→　反対の左向きに2進む
→　答えは3

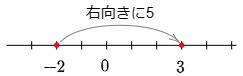
例2　(－2)＋5

　　数直線上の－2をとる
→　そこから右向きに5進む
→　答えは3

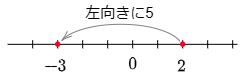
例3　2＋(－5)

　　数直線上の2をとる
→　そこから右向きに－5進む
→　反対の左向きに5進む
→　答えは－3

例4　(－5)＋2

　　数直線上の－5をとる
→　そこから右向きに2進む
→　答えは－3

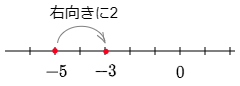
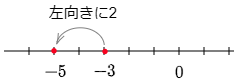
例5　(－3)＋(－2)

　　数直線上の－3をとる
→　そこから右向きに－2進む
→　反対の左向きに2進む
→　答えは－5

　私たちが普段「足す」という言葉を使うとき，それは基本的には増やすということを意味して用います。数直線では右側に行くイメージです。しかし数学ではこれらの計算例から分かるように，負の数を足すということは，数直線上で左向きに進むということを意味します。つまり減らすという意味です。負の符号である「－」は，計算において「進む向きを反対にする」という意味で捉えておくと，今後の計算の理解に大いに役立つでしょう。

2.2 減法

　引き算のことを減法(げんほう)といいます。例えば5－2のような計算です。この答えは3ですが，3をこの減法の差(さ)といいます。0以上の2つの数で大きい方から小さい方を引く計算は小学校で学習済みですから，ここでの話題はそれ以外の場合の計算です。そしてここでも数直線が威力を発揮します。

　加法のときと違って，減法では少しだけ注意が必要です。A－Bの「－」は，数直線上を「左向きに進め」の意味となります。

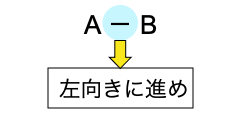
　このとき，減法は数直線を用いて次のように計算します。

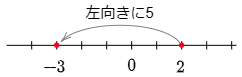
例6　2－5

　　数直線上の2をとる
→　そこから左向きに5進む
→　答えは－3

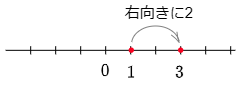
例7　1－(－2)

　　数直線上の1をとる
→　そこから左向きに－2進む
→　反対の右向きに2進む
→　答えは3

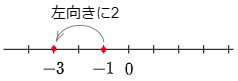
例8　－1－2

　　数直線上の－1をとる
→　そこから左向きに2進む
→　答えは－3

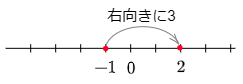
例9　－1－(－3)

　　数直線上の－1をとる
→　そこから左向きに－3進む
→　反対の右向きに3進む
→　答えは2

　私たちが普段「引く」という言葉を使うとき，それは基本的には減らすということを意味して用います。数直線では左側に行くイメージです。しかし数学ではこれらの計算例から分かるように，負の数を引くということは，数直線上で右向きに進むということを意味します。つまり増やすという意味です。加法のときがそうであったように，負の符号である「－」は，計算において「進む向きを反対にする」という意味で捉えておくのが良いでしょう。

演習1　次の計算をしなさい。
(1)　(－3.5)＋(＋2.7)
(2)　(10.2)－(－5.6)
(3)　(－2.61)－(＋4.09)
(4)　$\left(+\dfrac37\right)+\left(-\dfrac47\right)$
(5)　$\left(-\dfrac{13}6\right)+\left(-\dfrac52\right)$
(6)　$\left(-\dfrac1{12}\right)-\left(-\dfrac23\right)$