高校数学[総目次]
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [会員] | [会員] | |
| 2. 三角比の相互関係 | [会員] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |

1.正接・正弦・余弦
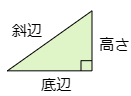
以下での考察の対象は直角三角形である.図のように直角三角形の直角が右下にくるように配置したとき,斜辺以外の残りの2つの辺を底辺,高さと呼ぶことにしよう.これら3つの辺から2本を選ぶ組合せは
{底辺,高さ},{斜辺,高さ},{斜辺,底辺}
の3通りある.そしてこれらの組から
高さ底辺,高さ斜辺,底辺斜辺
という分数を考え,順に正接(せいせつ),正弦(せいげん),余弦(よげん)と呼ぶ.これら3つを三角比というのである.
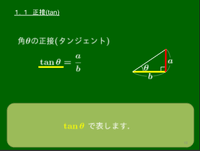
1.1 正接(tan)
正接とは何か~まずは具体例から
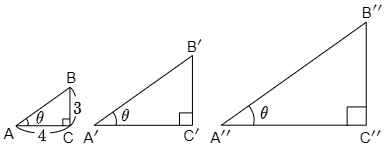
図の3つの直角三角形ABC,A′B′C′,A′′B′′C′′ は,左下の角の大きさがどれも θ (シータ) であるから,どの直角三角形もこの θ と直角(90°)の2つの角が共通している.従って「2組の角がそれぞれ等しい」という相似条件により,これら3つの直角三角形はすべて相似である.
※ θ はギリシャ文字である.読み方は「シータ」.
これら3つの相似な直角三角形の相似比(つまり辺の長さの比)が,例えば 1:2:3 だとすれば,斜辺以外の辺の長さは下図のようになっているであろう.
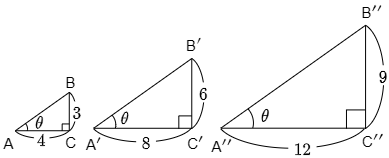
ここで 高さ底辺 を計算してみると左から順に
34,68,912
となり,約分すれば皆同じ値となる.今 1:2:3 の場合を見ただけにすぎないが,いかなる相似比であろうと,左下の角の大きさが θ であるような直角三角形ならこの 高さ底辺 は同じ値となることが理解できよう.すなわち直角三角形の 高さ底辺 の値は,三角形の大きさにはよらず,左下の角 θ のみによって決まるのだ.
この 高さ底辺 の値である 34 を指して「角 θ の正接」というのである.
正接とは何か~続いて一般論
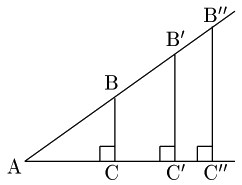
上の図において,3つの直角三角形ABC,AB′C′,AB′′C′′ は,∠Aが共通であるからすべて相似である(相似条件は「2組の角がそれぞれ等しい」).従って
BCAC=B′C′AC′=B′′C′′AC′′
が成り立つ.この比(分数)の値は直角三角形の大きさにはよらず,∠Aの大きさのみで決まる.
図の ∠A について,直角三角形の 高さ底辺 を ∠A の正接(せいせつ,タンジェント,tangent)という.
定義 正接(tan)
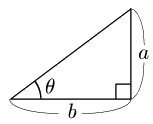
図において,ab を角θの正接 といい,tanθ で表す: tanθ=ab
覚え方
tanθ は,θ の角が左下に,直角が右下にくるように三角形を配置させたのち,tan の「 t 」を筆記体で書く順序で比を作ると得られる.(次のアニメーションを参照)
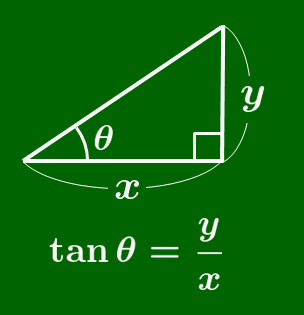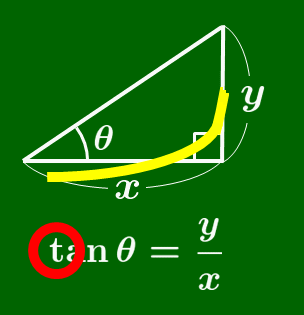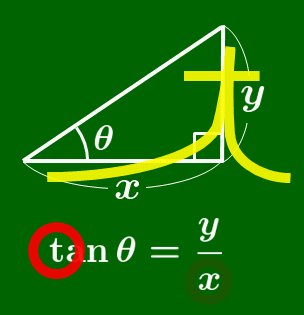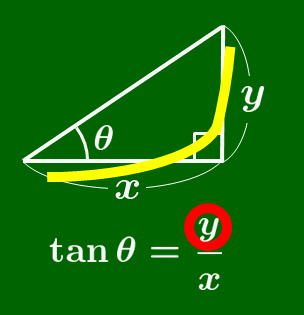
tan の覚え方
筆記体の t を書く要領
三角比を考えるときは
θ を左下へ,直角を右下へ
例
次の3つの直角三角形は,3つの辺の比が簡単な値であることから特別な直角三角形として最もよく利用される.辺の比が図のようになることは三平方の定理(の逆)から確認できる.
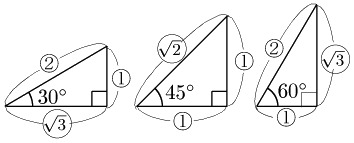
tan30∘=1√3,tan45∘=1,tan60∘=√3

補足1
tanは有理化しないこともある
tan の値は,例えば tan30∘=1√3 のように分母を有理化しないことも多い.この理由としては,√33 よりも表現がシンプルであることや,1√3 の方が上の図のような直角三角形の辺の比をイメージしやすいことなどが考えられる.
補足2
辺の長さをtanで表す
次の2つの式は tan の分母を払っただけのものであるが,辺の長さを tan で表現したものとして今後用いられる場面がある.
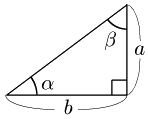
tanα=ab より,a=btanα
tanβ=ba より,b=atanβ

1.2 正弦(sin)・余弦(cos)
正弦,余弦とは何か

tan のときと同様に三角形の相似を考えると
BCAB=B′C′AB′=B′′C′′AB′′
ACBA=AC′B′A=AC′′B′′A
といった比の値(分数)が,直角三角形の大きさによらず,∠Aの大きさのみで決まる.
図の ∠A について,直角三角形の 高さ斜辺 を ∠A の正弦(せいげん,サイン,sine)といい,底辺斜辺 を ∠A の余弦(よげん,コサイン,cosine)という.
定義 正弦(sin)・余弦(cos)
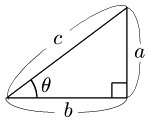
図において,
ac を,角θの正弦 といい,sinθ で表す.
bc を,角θの余弦 といい,cosθ で表す. sinθ=accosθ=bc
覚え方
tanθ のときと同様にして,θ の角が左下に,直角が右下にくるように三角形を配置させたのち,sin ならば「 s 」を筆記体で書く順序で,cos ならば「 c 」を書く順序で,比を作ると得られる.(次のアニメーションを参照)
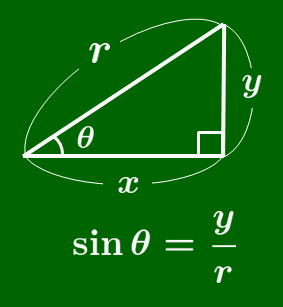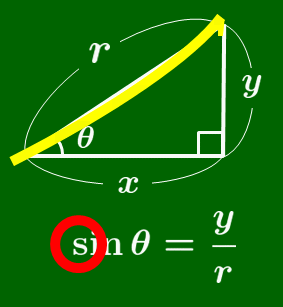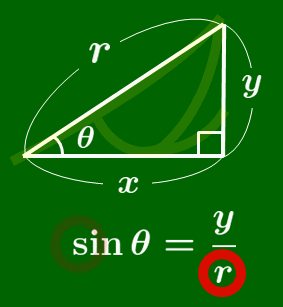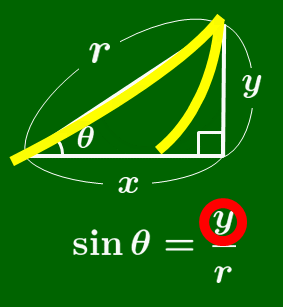
sin の覚え方
筆記体の s を書く要領
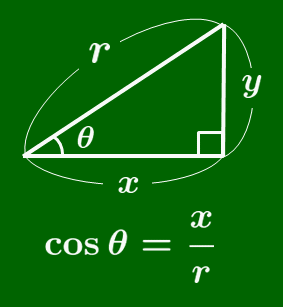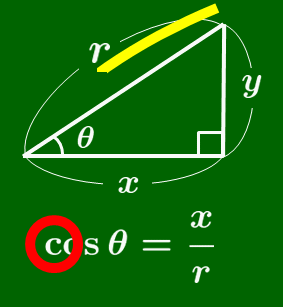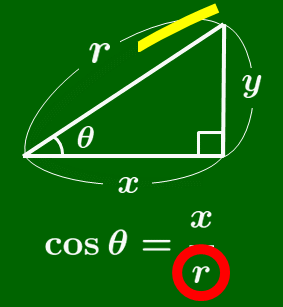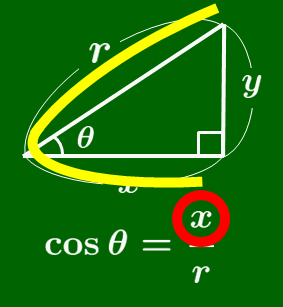
cos の覚え方
筆記体の c を書く要領
三角比を考えるときは
θ を左下へ,直角を右下へ
例
sin, cos も tan のときと同様に,次の特別な直角三角形における角が最もよく利用される.

sin30∘=12sin45∘=1√2sin60∘=√32cos30∘=√32cos45∘=1√2cos60∘=12
よく用いられる三角比の値
tanθ も含めて表にすると次のようになる:
| θ | 30° | 45° | 60° |
| sinθ | 12 | 1√2 | √32 |
| cosθ | √32 | 1√2 | 12 |
| tanθ | 1√3 | 1 | √3 |
ほとんどすべての角度の三角比は簡単には求められない
すぐ上の表にある30°,45°,60°以外の三角比の値は,簡単に求めることはできない.例えばsin17∘ の正確な値を,直角三角形の辺の長さから求めようと思ってもそれは無理な話である.どの数学Ⅰの教科書の巻末にも,1° 刻みで三角比の値の近似値が表になって与えられている.

補足
辺の長さをsin, cosで表す
次の2つの式は tan のときと同様に分母を払っただけのものであるが,辺の長さを sin, cos で表現したものとして今後用いられる場面がそれなりにある.

sinθ=ac より,a=csinθ
cosθ=bc より,b=ccosθ

次は,2.三角比の相互関係
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
数学Ⅰ 第2章 三角比
| スライド | ノート | 問題 | |
| 1. 正接,正弦,余弦 | [会員] | [会員] | |
| 2. 三角比の相互関係 | [会員] | [会員] | |
| 3. 三角比の拡張 | [会員] | ||
| 4. 正弦定理 | [会員] | [会員] | |
| 5. 余弦定理 | [会員] | [会員] | |
| 6. 三角形の面積 | [会員] | [会員] |