2次関数のグラフの移動を学習します.
まず,どんな2次関数 y=ax2+bx+c のグラフも,y=ax2 のグラフと合同であることを確認します.
次に,任意に与えられた2次関数 y=ax2+bx+c のグラフについて,平行移動,線対称移動,点対称移動を見ます.
それぞれにおいては,①頂点の移動とグラフの凸性を考える方法と,②グラフ上の任意の点が移動したあとの点を調べる方法の2パターンを考察します.
数学Ⅰ 第1章 2次関数
| スライド | ノート | 問題 | |
| 1. 2次関数のグラフ | [無料] | [会員] | |
| 2. 関数のグラフの移動 | [会員] | [会員] | |
| 3. 2次関数の最大・最小 | [会員] | [会員] | |
| 4. 2次関数の決定 | [会員] | [会員] | |
| 5. 2次関数のグラフと方程式 | [会員] | [会員] | |
| 6. 2次不等式とグラフ | [会員] | [会員] | |
| 7. 2次方程式の解の配置 | [会員] | [会員] |

2.関数のグラフの移動
| 2.1 放物線の合同 | スライド① |
| 2.1 放物線の合同(続き) | スライド② |
| 2.2 直線x=p に関する対称移動 2.3 直線y=q に関する対称移動 |
スライド③ |
| 2.4 原点に関する対称移動 | スライド④ |
スライドはぜひ全画面表示で
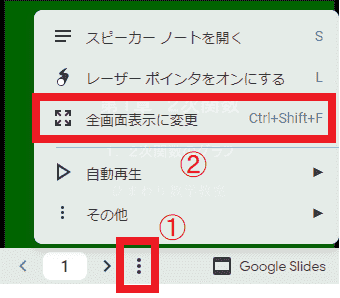
PC上では、下の図のようにスライド画面において、①→② とたどることで全画面表示にすることができます。PCでは画面も大きく、見やすさが全く異なります。
※ スマートフォン、タブレットでは全画面表示ができない場合があります。
スライドの切り替え
スライド画面の下にあるボタンでも切り替えができますが、次のような切り替え方があります:
PC:矢印ボタンの→や↓で「進む」、←や↑で「戻る」となります。
スマートフォン・タブレット:スライド画面をタップしたり、右から左にスワイプすれば「進む」、左から右にスワイプすると「戻る」となります。
※ iPhone など、一部のスマートフォン・タブレットでは、スライドの表示がスムーズでない場合があります。PC環境ではストレスなくスムーズに閲覧できますので、可能でしたらPCからの閲覧をお勧めします。
