高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [会員] | [会員] | |
| 2. メネラウスの定理 | [会員] | [会員] | |
| 3. チェバの定理の逆 | [会員] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |

1.垂心
定理
三角形の各頂点から対辺に引いた垂線は1点で交わる.
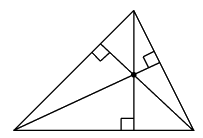
三角形の各頂点から対辺に引いた垂線は1点で交わる.

補足
定理中の3垂線の交点を垂心という.
証明の方針
・三角形の外側に,各辺とそれぞれ平行となる一回り大きい三角形をかく.
↓
・定理中の3垂線が,今作った三角形の各辺の垂直二等分線と一致することを示す.
(3辺の垂直二等分線が1点で交わることは,外心のところで証明済み.)
↓どうやって示すか?
図の中にある3つの平行四辺形を利用.
平行四辺形の性質
1. 対辺がそれぞれ平行
2. 対辺がそれぞれ等しい
証明
BC//QR,CA//RP,AB//PQ となる図のような△PQRを作る.
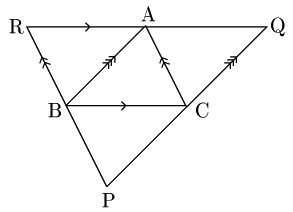

四角形ABCQ,ACBRは平行四辺形であるから, AQ=BC, AR=BC ∴AQ=AR よって,Aは辺QRの中点である.

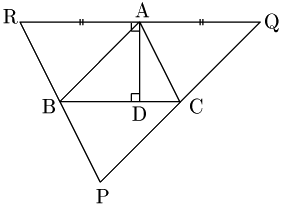
ここで,Aから対辺BCに垂線ADを引くと,BC//QRにより AD⊥QR 従って,ADは辺QRの垂直二等分線である.

同様にして,B,Cから対辺に引いた垂線についても,それぞれ辺RP,PQの垂直二等分線となる.つまり,△ABCにおける3つの垂線は,△PQRにおける垂直二等分線である.
3辺の垂直二等分線が1点で交わることは外心 のところで証明済みであるから,定理中の3垂線も1点で交わる.
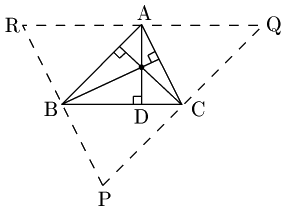
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [会員] | [会員] | |
| 2. メネラウスの定理 | [会員] | [会員] | |
| 3. チェバの定理の逆 | [会員] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |
