高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [会員] | [会員] | |
| 2. メネラウスの定理 | [会員] | [会員] | |
| 3. チェバの定理の逆 | [会員] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |

1.方べきの定理
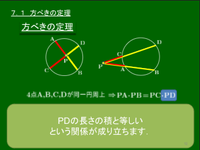
方べきの定理
下の図の①~③について,次が成り立つ:
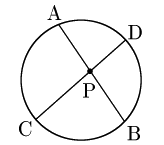
①弦が交点をもつとき
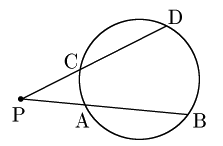
②弦の延長上に交点があるとき
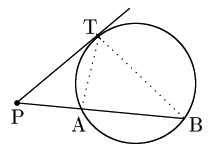
③Tが円の接点のとき
下の図の①~③について,次が成り立つ:



③:PTが△ABTの外接円の接線
(従ってTは接点)
⇒PA⋅PB=PT2
(従ってTは接点)
証明の方針
三角形の相似を示す.
↓
「対応する辺の比は等しい」を利用.
証明
①,②
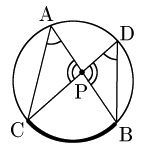
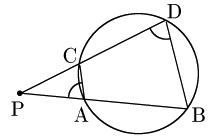
△PAC∽△PDB(∵2角相等)より PA:PD=PC:PB ∴PA⋅PB=PC⋅PD
③
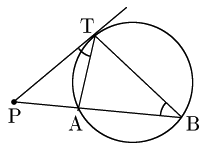
△PATと△PTBについて,∠Pは共通,接弦定理 により∠PTA=∠PBTであるから,△PAT∽△PTB (2角相等).よって, PA:PT=PT:PB ∴ PA⋅PB=PT2
■

2.方べきの定理の逆
方べきの定理の逆
下の図の①~③について,次が成り立つ: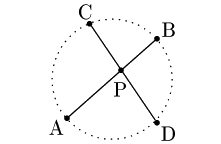
①ABとCDが交点をもつとき 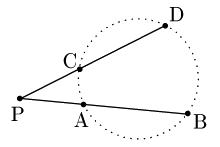
②AB,CDの延長上に交点があるとき
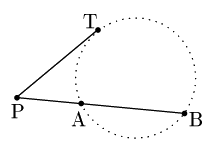
③
下の図の①~③について,次が成り立つ:



証明の方針
①と②
△ABCの外接円と半直線PDの交点D’をとる.
↓
DとD’が一致することを示す.
③
三角形の相似を示す.
↓
接弦定理の逆 を利用.
証明
①,②
△ABCの外接円と半直線PDとの交点をD’とする.
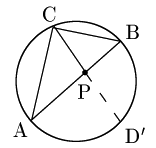
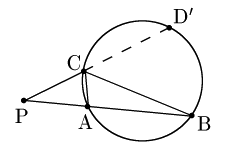
方べきの定理により
PA ⋅ PB = PC ⋅ PD’
また仮定より
PA ⋅ PB = PC ⋅ PD
従ってPD’=PDであるから,半直線PD上の2点DとD’は一致する.
よって,4点A,B,C,Dは同一円周上にある.
③
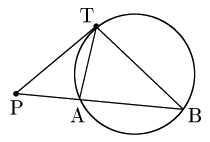
△PTAと△PBTにおいて,
∠Pは共通 ⋯ ①
仮定よりPA ⋅ PB = PT2であるから,
PAPT=PTPB
よって,
PA:PT = PT:PB ⋯ ②
①,②より,△PTA∽△PBT(∵2辺比夾角相等).
従って∠PTA = ∠PBTとなるから,接弦定理の逆 により,直線PTは円の接線である.
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学A 第3章 図形の性質
第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | [会員] | [会員] | |
| 2. メネラウスの定理 | [会員] | [会員] | |
| 3. チェバの定理の逆 | [会員] | ||
| 4. メネラウスの定理の逆 | [会員] | ||
| 5. 円に内接する四角形 | [会員] | [会員] | |
| 6. 接弦定理とその逆 | [会員] | ||
| 7. 方べきの定理とその逆 | [会員] | ||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | [会員] | ||
| 2. 円周角の定理の逆 | [会員] |