4. ド・モアブルの定理【ノート】
1人で学べる！高校数学

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート	問題
1. 複素平面
2. 複素数が表す図形
3. 極形式
4. ド・モアブルの定理
5. 複素数と図形

4. ド・モアブルの定理

4.1　ド・モアブルの定理とは

　極形式の節で学んだように，極形式で表された2つの複素数

$$z_1=r_1(\cos {\theta }_1+i\sin {\theta }_1),z_2=r_2(\cos {\theta }_2+i\sin {\theta }_2)$$

について，

$$z_1{z}_2=r_1{r}_2\{\sin ({\theta }_1+{\theta }_2)+i\sin ({\theta }_1+{\theta }_2)\}$$

となるから，$z=\cos \theta +i\sin \theta$ のとき，

$$\begin{array}{rl}{z}^2& =\cos (\theta +\theta )+i\sin (\theta +\theta )\\ & =\cos 2\theta +i\sin 2\theta \\ z^3& =z^2\cdot z\\ & =\cos (2\theta +\theta )+i\sin (2\theta +\theta )\\ & =\cos 3\theta +i\sin 3\theta \end{array}$$

　また， $$\begin{array}{rl}\frac{1}{z}& =\frac{\cos 0+i\sin 0}{\cos \theta +i\sin \theta }\\ & =\cos (0-\theta )+i\sin (0-\theta )\\ & =\cos (-\theta )+i\sin (-\theta )\\ \frac{1}{z^2}& =\frac{\cos 0+i\sin 0}{\cos 2\theta +i\sin 2\theta }\\ & =\cos (0-2\theta )+i\sin (0-2\theta )\\ & =\cos (-2\theta )+i\sin (-2\theta )\\ \frac{1}{z^3}& =\frac{\cos 0+i\sin 0}{\cos 3\theta +i\sin 3\theta }\\ & =\cos (0-3\theta )+i\sin (0-3\theta )\\ & =\cos (-3\theta )+i\sin (-3\theta )\end{array}$$

　従って，複素数 $z$，及び自然数 $n$ に対して，$z^{-n}$ を ${\displaystyle \frac{1}{z^n}}$，$z^0=1$ と定義すれば，一般に次が成り立つ：

ド・モアブルの定理　$n$ が整数のとき， $$(\cos \theta +i\sin \theta {)}^n=\cos n\theta +i\sin n\theta$$

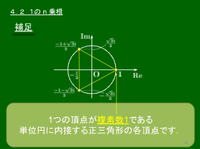
4.2　1の $n$ 乗根

※ 「$n$ 乗根(累乗根)」についての復習はこちら．

　1の $n$ 乗根( $n$ 乗すると1になる数)を $z$ とする：

$$z^n=1$$

　すると，$|z{|}^n$ は $$|z{|}^n=|z^n|=1$$ であり，$|z|$ は非負の実数であるから，$|z|=1$．従って，$z$ は複素平面上の原点を中心とする単位円周上の点であるから，極形式で $z=\cos \theta +i\sin \theta$ とおけて， $$\begin{array}{rl}{z}^n& =1\\ ⟺\cos n\theta +i\sin n\theta & =\cos 0+i\sin 0\\ ⟺n\theta & =0+2k\pi (k\text{は整数})\\ ⟺\theta & =\frac{2k\pi }{n}\end{array}$$

$\cos$ と $\sin$ の周期は $2\pi$ であるから，$z=\cos {\displaystyle \frac{2k\pi }{n}}+i\sin {\displaystyle \frac{2k\pi }{n}}$ ($k$ は整数)のうち，異なるものは $$k=0,1,2,\cdots ,n-1$$ の $n$ 個である．

まとめ　1の $n$ 乗根は次の $n$ 個： $$\begin{array}{rl}\cos \frac{2k\pi }{n}& +i\sin \frac{2k\pi }{n}\\ & (k=0,1,2,\cdots ,n-1)\end{array}$$

---

高校数学[総目次]

数学Ⅲ　第4章　複素平面

	スライド	ノート	問題
1. 複素平面
2. 複素数が表す図形
3. 極形式
4. ド・モアブルの定理
5. 複素数と図形