空間のベクトル方程式(球面)をスライドやさしく解説

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学B　第1章　ベクトル

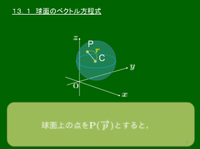
13．空間のベクトル方程式

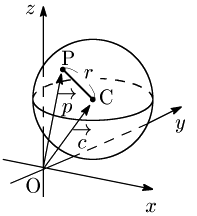
　定点 $C (\vec{c})$ から一定の距離 $r$ にある点の集合は，点 $C$ を中心とした半径 $r$ の球となる．球面上の点を $P (\vec{p})$ とすると，

$| \vec{C P} | = r$

　よって，

$| \vec{p} - \vec{c} | = r$

　これを球面のベクトル方程式という．

　 $C (a, b, c)$ ， $P (x, y, z)$ のとき，

$\begin{aligned} | \vec{p} - \vec{c} |^{2} & = | (x - a, y - b, z - c) |^{2} \\ = (x - a)^{2} + (y - b)^{2} + (z - c)^{2} \end{aligned}$

となるから次が成り立つ：

　点 $(a, b, c)$ を中心とする半径 $r$ の球面の方程式は $(x - a)^{2} + (y - b)^{2} + (z - c)^{2} = r^{2}$ 　特に，中心が原点のとき， $x^{2} + y^{2} + z^{2} = r^{2}$

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第1章　ベクトル