8. 空間ベクトル(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]

8.　空間ベクトル

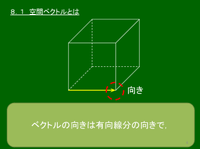
8.1　空間ベクトルとは

　向きと大きさだけを考え，位置を問題にしない空間内の量を空間ベクトルという．
　空間ベクトルの和，差，実数倍は，平面ベクトルと全く同様に計算できる．

空間ベクトルの演算\begin{align*} &[1]\ \ \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\ (\mbox{交換法則})\\[5pt] &[2]\ \ (\overrightarrow{a}\!+\!\overrightarrow{b})\!+\!\overrightarrow{c}\!=\!\overrightarrow{a}\!+\!(\overrightarrow{b}\!+\!\overrightarrow{c})\ (\mbox{結合法則})\\[5pt] &[3]\ \ \overrightarrow{a}+(-\overrightarrow{a})=\overrightarrow{0}\\[5pt] &\hspace{7mm}\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\\ &\hspace{7mm}\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\\[5pt] &[4]\ \ k,l\mbox{を実数として，}\\[5pt] &\hspace{8mm}k(l\overrightarrow{a})=(kl)\overrightarrow{a}\\[5pt] &\hspace{8mm}(k+l)\overrightarrow{a}=k\overrightarrow{a}+l\overrightarrow{a}\\[5pt] &\hspace{8mm}k(\overrightarrow{a}+\overrightarrow{b})=k\overrightarrow{a}+k\overrightarrow{b} \end{align*}

空間ベクトルの平行$\overrightarrow{a}\neq\overrightarrow{0},\ \overrightarrow{b}\neq\overrightarrow{0}$のとき，\[\overrightarrow{a}//\overrightarrow{b}\iff\overrightarrow{b}=k\overrightarrow{a}\mbox{となる実数}k\mbox{が存在}\]

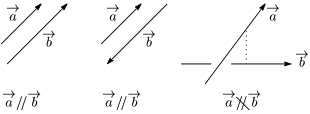
8.2　ベクトルの分解

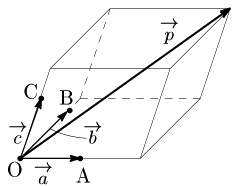
　4点O，A，B，Cは同一平面上にはないとし，$\overrightarrow{\mathstrut\rm OA}=\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut\rm OB}=\overrightarrow{\mathstrut b}$，$\overrightarrow{\mathstrut\rm OC}=\overrightarrow{\mathstrut c}$ とする．
　いま，空間内の任意の点 ${\rm P}(\overrightarrow{\mathstrut p})$ に対して，$\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut b}$，$\overrightarrow{\mathstrut c}$ に応じた平行六面体が一意に定まり，実数 $r,s,t$ を用いて

\[\overrightarrow{\mathstrut p}=r\overrightarrow{\mathstrut a}+s\overrightarrow{\mathstrut b}+t\overrightarrow{\mathstrut c}\]

と書ける．これは，$\overrightarrow{\mathstrut p}$ の $\overrightarrow{\mathstrut a}$，$\overrightarrow{\mathstrut b}$，$\overrightarrow{\mathstrut c}$ の3方向への分解を表している．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]

数学B　第1章　ベクトル

	スライド	ノート
1. ベクトルと有向線分	[無料]
2. ベクトルの演算	[無料]
3. ベクトルの成分	[無料]
4. ベクトルの内積	[会員]
5. 位置ベクトル	[会員]
6. ベクトル方程式	[会員]
7. 平面ベクトルの応用	[会員]
8. 空間ベクトル	[会員]
9. 空間ベクトルの成分	[会員]
10. 空間ベクトルの内積	[会員]
11. 空間の位置ベクトル	[会員]
12. 空間ベクトルの応用	[会員]
13. 空間のベクトル方程式	[会員]