高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | [無料] | ||
| 2. ベクトルの演算 | [無料] | ||
| 3. ベクトルの成分 | [無料] | ||
| 4. ベクトルの内積 | [会員] | ||
| 5. 位置ベクトル | [会員] | ||
| 6. ベクトル方程式 | [会員] | ||
| 7. 平面ベクトルの応用 | [会員] | ||
| 8. 空間ベクトル | [会員] | ||
| 9. 空間ベクトルの成分 | [会員] | ||
| 10. 空間ベクトルの内積 | [会員] | ||
| 11. 空間の位置ベクトル | [会員] | ||
| 12. 空間ベクトルの応用 | [会員] | ||
| 13. 空間のベクトル方程式 | [会員] | [会員] |

4. ベクトルの内積
ベクトル同士の掛け算をどう定義するか
ベクトルという分野のつまずきポイントを個人的に分析すれば,まず最初の関門が「ベクトルの差」であり,次がこの「ベクトルの内積」であろうと思われる.
これまでにベクトルの演算として登場したものは次の3つである:
①ベクトルの和(ベクトル同士の足し算)
②ベクトルの差(ベクトル同士の引き算)
③ベクトルの実数倍(ベクトルと実数の掛け算)
ここでは新たに,ベクトル同士の掛け算とでもいうべき内積についてみていこう.
私たちが2×3=6というとき,例えば長さ2mの木の枝を3本並べると合計6mになるといった具体的なイメージがつかめる.これに近いベクトルの概念は,すぐ上の③にあるベクトルの実数倍である.|→a|=2 であるベクトル →a に対して,3→a の大きさは2×3=6である.
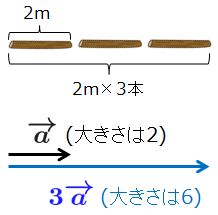
数字どうしの掛け算は,ベクトルでいえば実数倍に相当する
しかしこれから導入しようとしている内積は,この描像とは全く異なっている.そもそも内積は最早ベクトルではない.内積という装置に2つのベクトルを入力して出力されてくるものは1つの数字である.では得られた数字は一体何を意味するのであろうか.
2つのベクトルから抽出されたエッセンスをもとに精製された内積という不思議な数字について解説していこう.
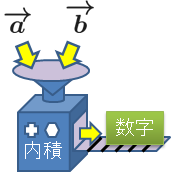
内積によって2つのベクトルから1つの実数が得られる
4.1 内積
ベクトルとは大きさと向きをもった量であった.ベクトル同士の掛け算を導入するとき,この大きさと向きという2つの量をどのように取り扱うのであろうか.
まず大きさについてはそのまま内積計算でも利用する.一方,向きについてはそれぞれの向きがそのまま利用されるのではなく,次の説明する2つのベクトルの「なす角」を利用するのである.
ベクトルのなす角
2つのベクトルのなす角は始点をそろえてできる角
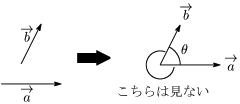
2つのベクトル →(a と →(b について,2つの始点が一致するように平行移動させたときにできる角(図のθ,ただし 0≦θ≦π)を,→(a と →(b のなす角という.
例 
△ABCは1辺の長さが2の正三角形.
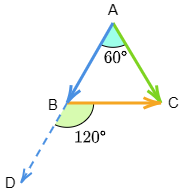
→AB と →AC のなす角は60°
→AB と →BC のなす角は,始点が異なっているから一致するように平行移動して120° (∠DBC)
内積
内積とはベクトル同士のある種の掛け算
さて準備は整った.いよいよ2つのベクトル同士の掛け算ともいうべき内積を説明していこう.
内積では2つのベクトルの大きさと、すぐ上で見た「なす角」を用いて計算する.しかし「なす角」の方はそのままの値を使うのではなく,なす角の余弦(cos,コサイン)を用いる.
→(a と →(b のなす角を θ とするとき, |→(a||→(b|cosθ を \boldsymbol{\overrightarrow{\mathstrut a}} と \boldsymbol{\overrightarrow{\mathstrut b}} の内積といい, \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b} で表す:
ベクトルの内積 \overrightarrow{\mathstrut a} と \overrightarrow{\mathstrut b} のなす角を \theta とするとき, \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta
補足
\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut 0} または \overrightarrow{\mathstrut b}=\overrightarrow{\mathstrut 0} のとき,2つのベクトルのなす角を考えることはできないが,\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=0 と定めておく.
例 
2つのベクトル \overrightarrow{\mathstrut a},\ \overrightarrow{\mathstrut b} について,|\overrightarrow{\mathstrut a}|=2,\ |\overrightarrow{\mathstrut b}|=3 とする.
① \overrightarrow{\mathstrut a} と \overrightarrow{\mathstrut b} のなす角が60°のとき
\overrightarrow{\mathstrut a}\cdot \overrightarrow{\mathstrut b}=|\overrightarrow{\mathstrut a}|\,|\overrightarrow{\mathstrut b}|\cos60^\circ=2\cdot3\cdot\frac12=3
② \overrightarrow{\mathstrut a} と \overrightarrow{\mathstrut b} のなす角が150°のとき
\overrightarrow{\mathstrut a}\cdot \overrightarrow{\mathstrut b}=|\overrightarrow{\mathstrut a}|\,|\overrightarrow{\mathstrut b}|\cos150^\circ=2\cdot3\cdot\left(-\frac{\sqrt3}2\right)=-3\sqrt3
さて,2つのベクトル\overrightarrow{\mathstrut a} と \overrightarrow{\mathstrut b} の内積を,\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta で計算することはわかったが,なんとも初学者にとってとっつきにくく,上で計算した3や -3\sqrt3 といった数字が何を意味しているかがわかりにくい.ここでこれらの数字の意味を図形的に提示する方法があるにはある.このページの下 4.5節の正射影 の考え方が,正に内積の図形的な意味を表すものなのであるが,実に残念なことに,それを知ったところで「ようし,内積がわかったぞ」という風にはなりにくい.正射影の考え方はむしろ内積が不自由なく使えるようになったあとで,入試問題などの応用問題に利用するという流れである.私の考えでは,学習の初段階では内積が何たるかを理解するのは脇へ置いておき,
差し当たって我慢する
というのが内積を理解する早道である.我慢をして計算練習を重ねて,とにかく意味は分からなくとも計算だけはできるようになっておくということである.数学の内容にはあとになってその意味や使い方がよくわかるようになるということはよくあって,内積もそういった事柄の一つではないかと感じる.内積はベクトルを学習している間は常に登場し続けるので,今後何十回,何百回と内積計算を行うことになるであろう.その過程の中で,自然と内積が自分の中で消化されていくというのが多くの人がたどる経過ではなかろうか.
内積について学習のヒントを少しだけ述べておくと,内積が使われる場面の代表的な2つの例として,ひとつは2つのベクトルのなす角が90°であるという条件があるとき,そしてもうひとつはすぐ下で説明するベクトルの大きさを計算するとき,この2つがある.前者では内積の値が0であるかそうでないかだけが問題となり,後者は内積の値がベクトルの大きさの2乗を表すのである.

重要事項 自分自身との内積は大きさの2乗を表す
同じベクトルのなす角は0°である.よって \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut a}=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut a}|\cos 0^\circ=|\overrightarrow{\mathstrut a}|^2 であるから,
重要 |\overrightarrow{\mathstrut a}|^2=\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut a}\ \ \ \left(|\overrightarrow{\mathstrut a}|=\sqrt{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut a}}\ \right)
これはベクトルの大きさの2乗が知りたければ,自分自身との内積を計算すればよいということを意味している.あるいはこの式の右辺から左辺への変形を考えて,自分自身との内積は大きさの2乗に等しいということを述べている.これは大変重要な公式であることを強調しておく.

4.2 内積と成分
内積を成分で表すとシンプルこの上ない式となる
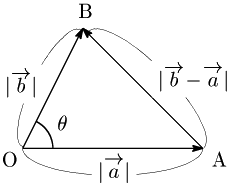
△OABにおいて,\overrightarrow{\mathstrut\rm OA}=\overrightarrow{\mathstrut a}=(a_1,a_2),\overrightarrow{\mathstrut\rm OB}=\overrightarrow{\mathstrut b}=(b_1,b_2) とし,\overrightarrow{\mathstrut a} と \overrightarrow{\mathstrut b} のなす角を \theta とする.
余弦定理により,
{\rm AB}^2={\rm OA}^2+{\rm OB}^2-2{\rm OA}\cdot{\rm OB}\cos\theta
この式は,\theta=0^\circ や 180^\circ のときも成り立つ.ベクトルで表せば,
|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2=|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-2\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}
\begin{align*}
\therefore \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}&=\frac{|\overrightarrow{\mathstrut a}|^2+|\overrightarrow{\mathstrut b}|^2-|\overrightarrow{\mathstrut b}-\overrightarrow{\mathstrut a}|^2}2\\[5pt]
&=\frac{({a_1}^2\!+\!{a_2}^2)\!+\!({b_1}^2\!+\!{b_2}^2)\!-\!\{(b_1\!-\!a_1)^2\!+\!(b_2\!-\!a_2)^2\}}2\\[5pt]
&=\frac{2(a_1\,b_1+a_2\,b_2)}2\\[5pt]
&=a_1\,b_1+a_2\,b_2
\end{align*}
これは,\overrightarrow{\mathstrut a}=\overrightarrow{\mathstrut 0},または \overrightarrow{\mathstrut b}=\overrightarrow{\mathstrut 0} のとき,即ち (a_1,a_2)=(0,0),または (b_1,b_2)=(0,0) のときも成立.
内積と成分 \overrightarrow{\mathstrut a}=(a_1,\ a_2),\overrightarrow{\mathstrut b}=(b_1,\ b_2) のとき, \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}=a_1\,b_1+a_2\,b_2

4.3 ベクトルのなす角
内積からは,なす角が直接求まるのではなくその余弦が求まる
\overrightarrow{\mathstrut 0} でない2つのベクトル \overrightarrow{\mathstrut a}=(a_1,a_2),\overrightarrow{\mathstrut b}=(b_1,b_2) のなす角を \theta とすると, \overrightarrow{\mathstrut a}\cdot \overrightarrow{\mathstrut b}=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta \begin{align*} \therefore\ \cos\theta&=\frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|}\\[5pt] &=\frac{a_1b_1+a_2b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}} \end{align*}
ベクトルのなす角と内積 \overrightarrow{\mathstrut 0} でない2つのベクトル \overrightarrow{\mathstrut a}=(a_1,a_2),\overrightarrow{\mathstrut b}=(b_1,b_2) のなす角を \theta とすると, \begin{align*} \therefore\ \cos\theta&=\frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|}\\[5pt] &=\frac{a_1b_1+a_2b_2}{\sqrt{{a_1}^2+{a_2}^2}\sqrt{{b_1}^2+{b_2}^2}} \end{align*}
例題 \overrightarrow{a}=(-1,\ -2),\ \overrightarrow{b}=(3,\ 1) のなす角 \theta を求めよ.
こたえ
\begin{align*} \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}&=-1\cdot3+(-2)\cdot1=-5\\[5pt] |\overrightarrow{\mathstrut a}|&=\sqrt{(-1)^2+(-2)^2}=\sqrt5\\[5pt] |\overrightarrow{\mathstrut b}|&=\sqrt{3^1+1^2}=\sqrt{10} \end{align*} よって, \cos\theta=\dfrac{-5}{\sqrt5\,\sqrt{10}}=-\dfrac1{\sqrt2} 0^\circ\leqq\theta\leqq180^\circ より,\underline{\boldsymbol{\theta=135^\circ}}
ベクトルの垂直
これぞ内積の最頻出利用法 – ベクトルで垂直とくれば内積取って0!
\overrightarrow{\mathstrut{a}} と \overrightarrow{\mathstrut{b}} のなす角が 90^\circ のとき,「\overrightarrow{\mathstrut{a}} と \overrightarrow{\mathstrut{b}} は垂直である」といい, \overrightarrow{\mathstrut{a}}\perp \overrightarrow{\mathstrut{b}} で表す.
\overrightarrow{\mathstrut{a}}\perp \overrightarrow{\mathstrut{b}} のとき,\cos90^\circ=0 であるから, \overrightarrow{\mathstrut{a}}\cdot \overrightarrow{\mathstrut{b}}=|\overrightarrow{\mathstrut{a}}|\,|\overrightarrow{\mathstrut{b}}|\cos90^\circ=0
逆に\overrightarrow{\mathstrut{a}}\cdot \overrightarrow{\mathstrut{b}}=0 のとき,2つのベクトルのなす角を \theta とすると,
|\overrightarrow{\mathstrut{a}}|\,|\overrightarrow{\mathstrut{b}}|\cos\theta=0
よって,|\overrightarrow{\mathstrut{a}}|\neq0,かつ |\overrightarrow{\mathstrut{b}}|\neq0 ならば,\cos\theta=0.
0^\circ\leqq\theta\leqq180^\circ より,\theta=90^\circ.従って \overrightarrow{\mathstrut{a}}\perp\overrightarrow{\mathstrut{b}}.
以上により次が成り立つ:
ベクトルの垂直条件 \overrightarrow{\mathstrut{a}}\neq\overrightarrow{0} かつ\overrightarrow{\mathstrut{b}}\neq\overrightarrow{0} のとき, \overrightarrow{\mathstrut{a}}\perp\overrightarrow{\mathstrut{b}}\iff\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{b}}=0 \overrightarrow{\mathstrut{a}}=(a_1,a_2),\overrightarrow{\mathstrut{b}}=(b_1,b_2) と成分で表されているときは, \overrightarrow{a}\perp\overrightarrow{b}\iff a_1a_2+b_1b_2=0
注意
「\overrightarrow{\mathstrut{a}}\neq0 かつ \overrightarrow{\mathstrut{b}}\neq0 」の仮定がなければ,
\begin{align*} &\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{b}}=0\\[5pt] \iff&\overrightarrow{\mathstrut{a}}\perp\overrightarrow{\mathstrut{b}}\ \underline{\boldsymbol{{\rm or}\ \overrightarrow{\mathstrut{a}}=\overrightarrow{\mathstrut{0}}\ {\rm or}\ \overrightarrow{\mathstrut{b}}=\overrightarrow{\mathstrut{0}}\ \ }} \end{align*}
のように下線部の条件が追加される.

4.4 内積の性質
特に次の [2] \overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut a}=|\overrightarrow{\mathstrut a}|^2 に注意.それ以外は通常の文字式とほぼ同等に扱える
内積の性質\begin{align*} &[1]\ \ \overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{\mathstrut{a}}\ \ (\mbox{交換法則})\\[5pt] &[2]\ \ \overrightarrow{a}\cdot\overrightarrow{a}=\left|\overrightarrow{a}\right|^2\\[5pt] &[3]\ \ \overrightarrow{\mathstrut{a}}\cdot(\overrightarrow{b}+\overrightarrow{\mathstrut{c}})=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b}+\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[4]\ \ (\overrightarrow{\mathstrut{a}}+\overrightarrow{b})\cdot\overrightarrow{\mathstrut{c}}=\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{\mathstrut{c}}+\overrightarrow{b}\cdot\overrightarrow{\mathstrut{c}}\ \ (\mbox{分配法則})\\[5pt] &[5]\ \ (k\overrightarrow{\mathstrut{a}})\cdot\overrightarrow{b}=\overrightarrow{a}\cdot(k\overrightarrow{b})=k(\overrightarrow{\mathstrut{a}}\cdot\overrightarrow{b})\ \ (k\mbox{ は実数}) \end{align*}
証明
2つのベクトルのなす角を \theta とする.
[1] \begin{align*} (\mbox{左辺}) &=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut b}|\cos\theta\\[5pt] &=|\overrightarrow{\mathstrut b}||\overrightarrow{\mathstrut a}|\cos\theta\\[5pt] &=(\mbox{右辺}) \end{align*}
[2] \begin{align*} (\mbox{左辺}) &=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut a}|\cos0^\circ\\[5pt] &=|\overrightarrow{\mathstrut a}||\overrightarrow{\mathstrut a}|\\[5pt] &=(\mbox{右辺}) \end{align*}
[3] \overrightarrow{\mathstrut a}\!=\!(a_1,a_2),\overrightarrow{\mathstrut b}\!=\!(b_1,b_2),\overrightarrow{\mathstrut c}\!=\!(c_1,c_2) とすると, \begin{align*} (\mbox{左辺}) &=(a_1,a_2)\cdot(b_1+c_1,b_2+c_2)\\[5pt] &=a_1(b_1+c_1)+a_2(b_2+c_2)\\[5pt] &=(a_1b_1+a_2b_2)+(a_1c_1+a_2c_2)\\[5pt] &=(\mbox{右辺}) \end{align*}
[4]は,[3]と同様に示される.
([1]と[3]を用いて示してもよい.)
[5] \overrightarrow{\mathstrut a}\!=\!(a_1,a_2),\overrightarrow{\mathstrut b}\!=\!(b_1,b_2) とすると, \begin{align*} (\mbox{左辺})&=(ka_1,ka_2)\cdot(b_1,b_2)\\[5pt] &=ka_1b_1+ka_2b_2\\[5pt] &=\left\{ \begin{array}{l} a_1\!\times\! kb_1\!+\!a_2\!\times\! kb_2\!=\!(a_1,b_1)\cdot(kb_1,kb_2)\!=\!(\mbox{中辺})\\[5pt] k(a_1b_1+a_2b_2)=(\mbox{右辺}) \end{array}\right. \end{align*}
■
補足
[5]により,k(\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}) は簡単に k\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b} と書く.
注意
(\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b})\overrightarrow{\mathstrut c}=\overrightarrow{\mathstrut a}(\overrightarrow{\mathstrut b}\cdot\overrightarrow{\mathstrut c}) のような式は成り立たない.

4.5 内積と正射影
正射影ベクトルとは
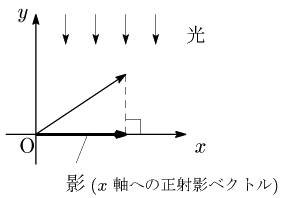
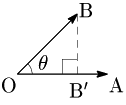
2つのベクトル \overrightarrow{\mathstrut\rm OA},\overrightarrow{\mathstrut\rm OB} のなす角 \theta が鋭角のとき,Bから直線OAに下ろした垂線の足を\rm B’とする.このとき \overrightarrow{\mathstrut\rm OB’} を
\overrightarrow{\mathstrut\rm OB} の \overrightarrow{\mathstrut\rm OA}(の上)への正射影ベクトル
という.
内積の図形的な意味
\cos\theta=\dfrac{\rm OB’}{\rm OB} より, \begin{align*} \overrightarrow{\mathstrut\rm OA}\cdot\overrightarrow{\mathstrut\rm OB}&=|\overrightarrow{\mathstrut\rm OA}||\overrightarrow{\mathstrut\rm OB}|\cos\theta\\[5pt] &={\rm OA}\cdot{\rm OB}\cdot\frac{\rm OB’}{\rm OB}\\[5pt] &={\rm OA}\cdot{\rm OB’} \end{align*} このことから,内積の図形的な意味は次のようになる:
内積の図形的な意味 \overrightarrow{\mathstrut 0} でない2つのベクトル \overrightarrow{\mathstrut\rm OA},\overrightarrow{\mathstrut\rm OB} のなす角が鋭角のとき,それらの内積は,\overrightarrow{\mathstrut\rm OA} の大きさと,\overrightarrow{\mathstrut\rm OB} の \overrightarrow{\mathstrut\rm OA} への正射影ベクトルの大きさとの積である.
重要例題
\overrightarrow{\mathstrut 0} でない2つのベクトル \overrightarrow{\mathstrut a},\overrightarrow{\mathstrut b} について,\overrightarrow{\mathstrut b} の \overrightarrow{\mathstrut a} への正射影ベクトル \overrightarrow{\mathstrut c} を,\overrightarrow{\mathstrut a},\overrightarrow{\mathstrut b} を用いて表せ.
答
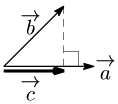
\overrightarrow{\mathstrut c}=k\,\overrightarrow{\mathstrut a} (k は実数)とおける.
\overrightarrow{\mathstrut a}\perp(\overrightarrow{\mathstrut c}-\overrightarrow{\mathstrut b}) より,\overrightarrow{\mathstrut a}\cdot(\overrightarrow{\mathstrut c}-\overrightarrow{\mathstrut b})=0.
\therefore \overrightarrow{\mathstrut a}\cdot(k\,\overrightarrow{\mathstrut a}-\overrightarrow{\mathstrut b})=0
\therefore k=\dfrac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}|^2}
故に,\underline{\boldsymbol{\overrightarrow{\mathstrut c}=\dfrac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}|^2}\overrightarrow{\mathstrut a}}}
正射影ベクトル \overrightarrow{\mathstrut 0} でない2つのベクトル \overrightarrow{\mathstrut a},\overrightarrow{\mathstrut b} について,\overrightarrow{\mathstrut b} の \overrightarrow{\mathstrut a} への正射影ベクトルは, \frac{\overrightarrow{\mathstrut a}\cdot\overrightarrow{\mathstrut b}}{|\overrightarrow{\mathstrut a}|^2}\overrightarrow{\mathstrut a}

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | [無料] | ||
| 2. ベクトルの演算 | [無料] | ||
| 3. ベクトルの成分 | [無料] | ||
| 4. ベクトルの内積 | [会員] | ||
| 5. 位置ベクトル | [会員] | ||
| 6. ベクトル方程式 | [会員] | ||
| 7. 平面ベクトルの応用 | [会員] | ||
| 8. 空間ベクトル | [会員] | ||
| 9. 空間ベクトルの成分 | [会員] | ||
| 10. 空間ベクトルの内積 | [会員] | ||
| 11. 空間の位置ベクトル | [会員] | ||
| 12. 空間ベクトルの応用 | [会員] | ||
| 13. 空間のベクトル方程式 | [会員] | [会員] |

