高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | [会員] | ||
| 2. ベクトルの演算 | [会員] | ||
| 3. ベクトルの成分 | [会員] | ||
| 4. ベクトルの内積 | [会員] | ||
| 5. 位置ベクトル | [会員] | ||
| 6. ベクトル方程式 | [会員] | ||
| 7. 平面ベクトルの応用 | [会員] | ||
| 8. 空間ベクトル | [会員] | ||
| 9. 空間ベクトルの成分 | [会員] | ||
| 10. 空間ベクトルの内積 | [会員] | ||
| 11. 空間の位置ベクトル | [会員] | ||
| 12. 空間ベクトルの応用 | [会員] | ||
| 13. 空間のベクトル方程式 | [会員] | [会員] |

3. ベクトルの成分
3.1 ベクトルの成分表示
目標
ベクトルを有向線分以外の方法で表す.
アイデア
座標平面に有向線分(矢印)を配置する.
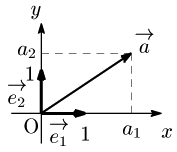
- 座標平面上の原点を始点とするベクトルで,終点が点(1,0) の →(e1 と,点(0,1) の →(e2 の2つを用意.
- 有向線分の始点が原点にくるよう平行移動.
- 終点の座標を (a1,a2) とすれば, →(a=a1→(e1+a2→(e2
つまり,常に始点を原点にとれば,
ベクトル ←1対1対応→ 終点の座標
そこで, →(a=(a1,a2) で表し,ベクトルの成分表示という.
成分表示されたベクトルに対して,相等と大きさは次のようになる:
ベクトルの成分表示 →(a=(a1,a2),→(b=(b1,b2) のとき,→(a=→(b⟺a1=b1 かつ a2=b2 |→(a|=√a12+a22
補足
→(a=(ka1,ka2) のとき,
|→(a|=|k|√a12+a22
注意
成分表示における等号「=」は必ず.
→(a(a1,a2) といった点の座標のようには書かない.

3.2 成分表示の和,差,実数倍
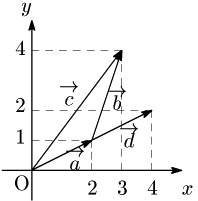
→(a=(2,1),→(b=(1,3),→(a+→(b を →(c とおくと,図より
→(c=(3,4)
一方,
→(c=→(a+→(b=(2,1)+(1,3)
であるから,
(2,1)+(1,3)=(2+1,1+3)
が成り立つ.
また,2→(a を →(d とおくと,図より
→(d=(4,2)
一方,
→(d=2→(a=2(2,1)
であるから,
2(2,1)=(2⋅2,2⋅1)
が成り立つ.
一般に次が成り立つ:
成分表示の和,差,実数倍[1] (a1, a2)+(b1, b2)=(a1+b1, a2+b2)[2] k(a1, a2)=(ka1, ka2) (k は実数)
証明
→(a=(a1,a2),→(b=(b1,b2) は,→(e1=(1,0),→(e2=(0,1) を用いて, →(a=a1→(e1+a2→(e2→(b=b1→(e1+b2→(e2 と表されるから, →(a+→(b=(a1+b1)→(e1+(a2+b2)→(e2=(a1+b1, a2+b2)→(a−→(b=(a1−b1)→(e1+(a2−b2)→(e2=(a1−b1, a2−b2)k→(a=ka1→(e1+ka2→(e2=(ka1, ka2)
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | [会員] | ||
| 2. ベクトルの演算 | [会員] | ||
| 3. ベクトルの成分 | [会員] | ||
| 4. ベクトルの内積 | [会員] | ||
| 5. 位置ベクトル | [会員] | ||
| 6. ベクトル方程式 | [会員] | ||
| 7. 平面ベクトルの応用 | [会員] | ||
| 8. 空間ベクトル | [会員] | ||
| 9. 空間ベクトルの成分 | [会員] | ||
| 10. 空間ベクトルの内積 | [会員] | ||
| 11. 空間の位置ベクトル | [会員] | ||
| 12. 空間ベクトルの応用 | [会員] | ||
| 13. 空間のベクトル方程式 | [会員] | [会員] |