高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | [無料] | ||
| 2. ベクトルの演算 | [無料] | ||
| 3. ベクトルの成分 | [無料] | ||
| 4. ベクトルの内積 | [会員] | ||
| 5. 位置ベクトル | [会員] | ||
| 6. ベクトル方程式 | [会員] | ||
| 7. 平面ベクトルの応用 | [会員] | ||
| 8. 空間ベクトル | [会員] | ||
| 9. 空間ベクトルの成分 | [会員] | ||
| 10. 空間ベクトルの内積 | [会員] | ||
| 11. 空間の位置ベクトル | [会員] | ||
| 12. 空間ベクトルの応用 | [会員] | ||
| 13. 空間のベクトル方程式 | [会員] | [会員] |

2. ベクトルの演算
2.1 ベクトルの加法
「向き」と「大きさ」を同時に持つ量をベクトルと呼んだが,これらに実数のときにあったような加減乗除,すなわち足したり引いたり掛けたり割ったりといった計算ができるのであろうか.足し算・引き算はベクトルにも存在する.また,ある種の掛け算も存在する.しかしベクトルの割り算は存在しない.加減乗除のうち「加減乗」はあるが,「除」だけはないのである.
それではベクトルの足し算である加法からみていこう.
ベクトルどうしの足し算とは?
2つのベクトル →(a と →(b について,→(a+→(b のような量を考えたい.どのように導入すればよいだろうか.ベクトルには向きと大きさがあったから,大きさだけをみてその和を考えるのであろうか?
例として床に大きな荷物があるとしよう.これをAさんが右向きに4の力で引っ張ったが動かなかったので,通りかかったBさんに手伝いを求めた.そこでBさんは3の力で手伝ったところ,荷物が動き出した.このとき,2人は合計で4+3=7の力で引っ張ったことになる.
それでは次はどうだろう.机の上に消しゴムを置いて,右向きに4の力で引っ張り,同時に上向きに3の力で引っ張るとしよう.さてこの消しゴムはどの方向にどんな力で引っ張られて行くであろうか.実はこのとき,対角線の方向に5の力で引っ張られることになる.単純に4+3で7とはならない.また次のように述べることもできる.この消しゴムに対して右方向に4,上方向に3という2つの力を加えることと,対角線の方向に5という力を1つだけ加えることは,消しゴムに対して全く同じ作用を与えることになる.

1つの力だけで表すことができる.
ベクトルの加法とは
先の消しゴムの例で見たように,ある物体に対して異なる向きに2つの力を加えると,その2つのどちらとも異なる向きに力を加えていることになる.その向きとは消しゴムの例では長方形の対角線の方向であったが,一般には2つの力の向きを2辺とする平行四辺形の対角線の方向になる.そして力の大きさは対角線の長さとなる.これを数学的に表現したものがベクトルの足し算である加法だ.
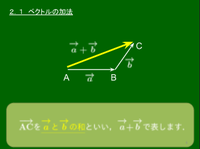
2つのベクトル →(a,→(b について,それらを始点をそろえて有向線分で表したとき,その2辺でできる平行四辺形の向き付き対角線を →(a と →(b の和といい,→(a+→(b で表す.
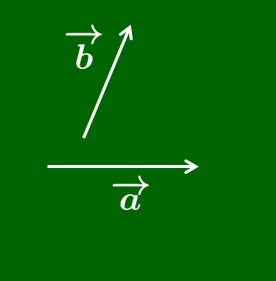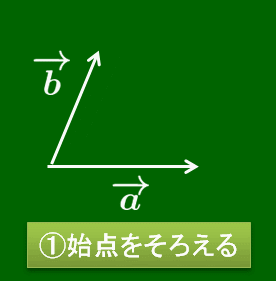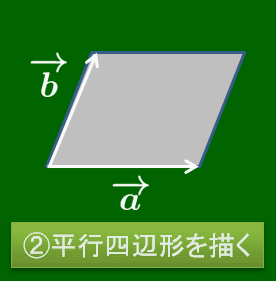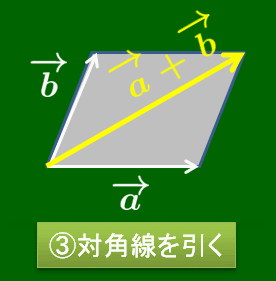
あるいは次のように考えることもできる.ベクトルは描く位置にはよらなかったので,→(a の終点に →(b の始点を重ね,→(a の始点から→(b の終点に伸びる有向線分が表すベクトルを →(a と →(b の和といって,→(a+→(b で表すのだ.
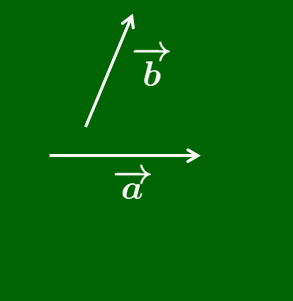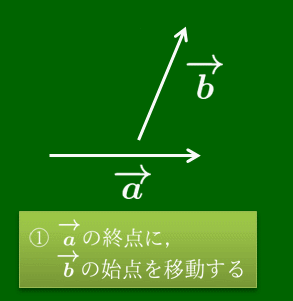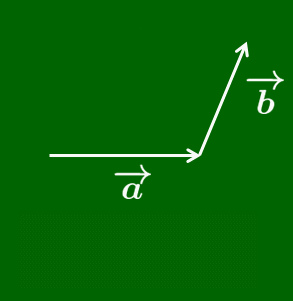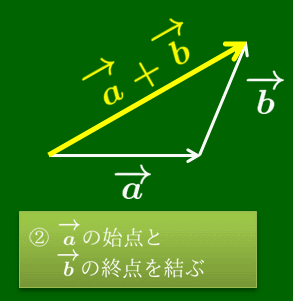
ベクトルの加法 →(a=→(AB,→(b=→(BC のとき,→(AC を →(a と →(b の和といい, →(a+→(b で表す.
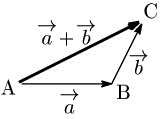
例
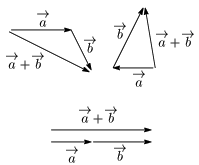
これらの例からもわかるように,一般には |→(a+→(b|≦|→(a|+|→(b| であって,等号が成り立つというのは →(a と →(b が同じ向きのとき,またそのときに限るのである.A地点からC地点に向かう経路の中で,AからCまでまっすぐに結ぶものが最短だというのは誰しも納得するところであろう.
加法の性質
2つのベクトルの和について定義したが,これらの和について,実数のときに成り立っていた次の性質がベクトルでも成り立つ.
[1] →a+→b=→b+→a (交換法則)
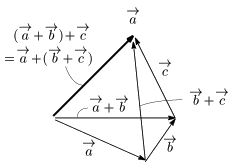
[2] (→a+→b)+→c=→a+(→b+→c) (結合法則)
これらの性質が成り立つことを,次の例を通して理解しておこう.
[1]
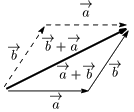
[2]
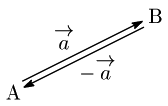
逆ベクトル
→(a と
大きさ:同じ
向き :反対
のベクトルを,→(a の逆ベクトルといい,−→(a で表す:
注意
ベクトルでは「+,−」は正負の意味ではなく,向きを表す.
零ベクトル
始点と終点が一致するベクトルを零ベクトルといい,→(0 で表す.
注意
→(0 の大きさは0,向きは考えない.
−→aと→0の性質[1]→a+→0=→0+→a=→a[2]→a+(−→a)=(−→a)+→a=→0
[2]について
→(a=→(AB とすると,
→(a+(−→(a)=→(AB+→(BA=→(AA=→(0

2.2 ベクトルの減法
→(a+(−→(b) を →(a と →(b の差といい, →(a−→(b で表す:
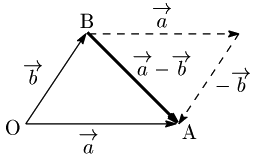
例
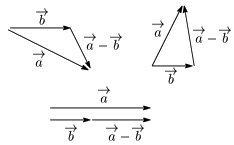

2.3 ベクトルの実数倍
→(a と実数 k に対して,k→(a を次のように定める:
1° →(a≠→(0 のとき
| k>0 | k<0 | |
| 大きさ | |→(a| の k 倍 | |→(a| の |k| 倍 |
| 向き | →(a と同じ | →(a と反対 |
また,k=0 のときは,→(0 と定める.
2° →(a=→(0 のとき
任意の実数 k に対して, k→(a=→(0 と定める.
例
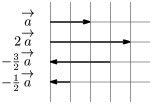
ベクトルの実数倍の性質 k, l が実数のとき,[1]k(l→a)=(kl)→a[2](k+l)→a=k→a+l→a[3]k(→a+→b)=k→a+k→b
[3]の証明
k>0 のとき
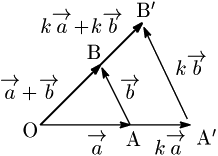
→OB と →OB′ について,△OAB∽△OA′B′ により,
k|→OB|=|→OB′|
そして向きも同じであることから,
k→OB=→OB′
従って
k(→(a+→(b)=k→(a+k→(b
が成り立つ.
k<0 の場合も同様にして示される.
補足
これまでの議論により,ベクトルの和,差,実数倍は,文字式と同じように扱えることがわかる.
例
5→a+→b−(3→a+4→b)=2→a−3→b
2(3→a−4→b)=6→a−8→b

2.4 ベクトルの平行
→(0 でない2つのベクトル →(a,→(b について,向きが同じ,または反対のとき,「→(a と →(b は平行である」といい, →(a//→(b で表す.
例
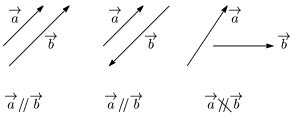
ベクトルの平行条件 →a≠→0, →b≠→0 のとき,→a//→b⟺→a=k→b (kは実数)
補足
→(a|→(a| は →(a と同じ向きに平行な単位ベクトルである.
∵)→(a|→(a|=1|→(a|→(a であり,1|→(a|>0 により,→(a と同じ向き.
また,
|→(a|→(a||=|→(a||→(a|=1
により,単位ベクトル.
■
→a(≠→0) に平行な単位ベクトルは, ±→a |→a|
次の定理はベクトルの問題を解く上で今後何度も登場する.
重要な定理 s, t, s′, t′ を実数とする. →a≠→0, →b≠→0で,→aと→bが平行でないとき, s→a+t→b=s′→a+t′→b⟺s=s′,t=t′ ⋯① 特に, s→a+t→b=→0⟺s=t=0 ⋯②
証明
まず②を示す.
⇐ は明らか.
⇒
s≠0 とすれば,→(a=−ts→(b.
これは →(a//→(b を意味し,矛盾.よって s=0.
このとき,t→(b=→(0 となり,→(b≠→(0 により t=0.
■
次に①を示す.
⇐ は明らか.
⇒
変形して,
(s−s′)→(a+(t−t′)→(b=→(0
よって②より,
s−s′=0, t−t′=0
∴s=s′, t=t′
■
補足
→(a,→(b がともに →(0 でなく,また平行でないとき,「→(a と →(b は1次独立である」という.

2.5 ベクトルの分解
あるベクトル →(p が与えられると,1次独立な2つのベクトルの2方向に分解できる.
例
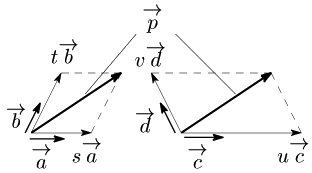
右は →(p=u→(c+v→(d
(s,t,u,v は実数)
→(p を s→(a+t→(b のように表すとき,これをベクトルの分解という.
任意のベクトル →(p に対して, →(p=s→(a+t→(b と表せるとき,上の定理 により実数 s,t は →(a と →(b に応じてただ1通りに決定する.即ち, {→(a=s→(a+t→(b→(a=s′→(a+t′→(b のような見かけ上異なる表現が取れたとしても実際は s=s′, t=t′ である.
ベクトルの分解 2つのベクトル →(a,→(b は→(0 ではなく,また平行でもないとする.このとき,任意のベクトル →(p は実数 s,t を用いて, →(p=s→(a+t→(b とただ1通りに表現できる.
補足
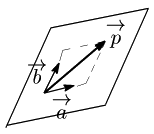
逆に1次独立な2つのベクトル →(a,→(b を決めると,→(a と →(b で張る平面上の任意のベクトル →(p は,実数 s,t を用いて, →(p=s→(a+t→(b の形でただ1通りに表すことができる.

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学B 第1章 ベクトル
| スライド | ノート | 問題 | |
| 1. ベクトルと有向線分 | [無料] | ||
| 2. ベクトルの演算 | [無料] | ||
| 3. ベクトルの成分 | [無料] | ||
| 4. ベクトルの内積 | [会員] | ||
| 5. 位置ベクトル | [会員] | ||
| 6. ベクトル方程式 | [会員] | ||
| 7. 平面ベクトルの応用 | [会員] | ||
| 8. 空間ベクトル | [会員] | ||
| 9. 空間ベクトルの成分 | [会員] | ||
| 10. 空間ベクトルの内積 | [会員] | ||
| 11. 空間の位置ベクトル | [会員] | ||
| 12. 空間ベクトルの応用 | [会員] | ||
| 13. 空間のベクトル方程式 | [会員] | [会員] |