高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | [会員] | ||
| 2. 一般角の三角関数 | [会員] | ||
| 3. 三角関数の性質 | [会員] | [会員] | |
| 4. 三角関数のグラフ | [会員] | ||
| 5. 三角関数の加法定理 | [会員] | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | ||
| 7. 三角関数の合成 | [会員] | ||
| 8. 三角関数の応用 | [会員] |

7.0 三角関数の合成とは
三角関数の合成とは何か
三角関数の合成公式と呼ばれるものがある.sin と cos の1次式を sin だけ,あるいは cos だけで書き表すもので,これは要するに sin,cos の加法定理 で,右辺から左辺への書き換えのことである.例えば sin の加法定理である
sin(α+β)=sinαcosβ+cosαsinβ
という式について,左辺と右辺を入れ替えた
sinαcosβ+cosαsinβ=sin(α+β)
が三角関数の sin による合成公式であると,大雑把に言うことができる.

7.1 sin での合成
asinθ+bcosθ を sin だけの式にする
sin の加法定理 である sin(α+β)=sinαcosβ+cosαsinβ において,右辺から左辺に書き換えるのが sin での合成である.
例 √3sinθ+cosθ=□sin(θ+△)
この左辺を変形して,右辺のように sin だけの式を導こう.それには □ と △ の情報が必要である.□ と △ の値を得るために,以下のような手順で変形を行う.
手順
- sin の係数である √3 と cos の係数である1の平方の和を計算し,正の平方根をとる.
√(√3)2+12=√4=2 - 手順1で求めた 2 で,式全体を無理矢理くくる.
√3sinθ+cosθ=2(sinθ⋅√32_①+cosθ⋅12_②) - sin(θ+α)=sinθcosα_①+cosθsinα_② (sinの加法定理)の右辺と比較して,cosα=√32 (①), sinα=12 (②)となるような角 α を探すと,α=π6 が当てはまる.
- sinの加法定理で右辺から左辺の書き換えを行って完了.
√3sinθ+cosθ=2(sinθcosπ6+cosθsinπ6)=2sin(θ+π6)

以上の流れを式だけで表すと次のようになる:
(左辺)=√(√3)2+12(sinθ⋅√32+cosθ⋅12)=√3+1(sinθ⋅cosπ6+cosθ⋅sinπ6_)=2sin(θ+π6)_
※ の部分で sin の加法定理を用いた.

一般に asinθ+bcosθ=√a2+b2(sinθ⋅a√a2+b2+cosθ⋅b√a2+b2)=√a2+b2sin(θ+α) ただし α は,
sinα=b√a2+b2, cosα=a√a2+b2
となる角である.
三角関数のsinでの合成公式asinθ+bcosθ=√a2+b2sin(θ+α)
ただし,sinα=b√a2+b2, cosα=a√a2+b2
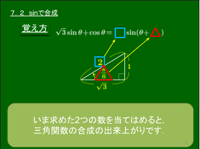
覚え方
三角関数を合成する際,上の手順書通りにやるとそれなりに手間がかかるが,実際には次のような考え方をとることで,慣れてくればほぼストレスフリーで合成完了までもっていけるようになる.
座標平面上に,sin の係数を x 座標に,cos の係数を y 座標にもつ点 (a,b) をとり,原点Oと結ぶ.この線分の長さ(図の□)が合成したときの sin の係数であり,線分と x 軸の正の向きとのなす角(図の△)が合成したときに用いる角である.
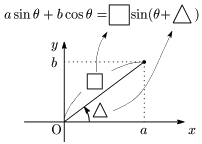
三角関数の合成ができる型
さて,三角関数が合成できる形は a,b を実数の定数として
asinθ+bcosθ
であって,
三角関数の合成ができる型
- sin,cos の1次式.
- sin,cos の中身 (ここでは θ とする) は同じ.
- sin,cos の係数 a,b は同じ数である必要なし.
- sin,cos の係数 a,b は正負いかなる数でもよい.
というのが特徴である.


例題 次の式を rsin(θ+α) の形に変形せよ.ただし,r>0,−π<α<π とする.
(1) −√3sinθ+cosθ
(2) −√3sinθ−cosθ
(3) √3sinθ−cosθ


7.2 cos での合成
asinθ+bcosθ を cos だけの式にする
sin で合成したものと同じ式である asinθ+bcosθ を,今度は cos で合成してみよう.
cos の加法定理 である cos(α−β)=cosαcosβ+sinαsinβ において,右辺から左辺に書き換えるのが cos での合成である.
※ cos(α+β) ではなく, cos(α−β) とマイナスになっていることに注意.下の「注意」も参照.
例 √3sinθ+cosθ=□cos(θ−△)
この左辺を変形して,右辺のように cos だけの式を導こう.それには □ と △ の情報が必要である.□ と △ の値を得るために,以下のような手順で変形を行う.
手順
- cosが前,sinが後ろになるように書き換えた上で,cos の係数である 1 と sin の係数である √3 の平方の和を計算し,正の平方根をとる.√12+(√3)2=√4=2
- 手順1で求めた 2 で,式全体を無理矢理くくる.
cosθ+√3sinθ=2(cosθ⋅12_①+sinθ⋅√32_②) - cos(θ−α)=cosθcosα_①+sinθsinα_② (cosの加法定理)の右辺と比較して,cosα=12 (①), sinα=√32 (②)となるような角 α を探すと,α=π3 が当てはまる.
- cosの加法定理で右辺から左辺の書き換えを行って完了.
cosθ+√3sinθ=2(cosθcosπ3+sinθsinπ3)=2cos(θ−π3)

以上の流れを式だけで表すと次のようになる:
(左辺)=cosθ+√3sinθ=√12+(√3)2(cosθ⋅12+sinθ⋅√32)=√1+3(cosθ⋅cosπ3+sinθ⋅sinπ3_)=2cos(θ−π3)_ ※ の部分で cos の加法定理を用いた.

一般に asinθ+bcosθ=bcosθ+asinθ=√b2+a2(cosθ⋅b√a2+b2+sinθ⋅a√a2+b2)=√a2+b2cos(θ−β) ただし β は, cosβ=b√a2+b2, sinβ=a√a2+b2 となる角である.
三角関数のcosでの合成公式asinθ+bcosθ=√a2+b2cos(θ−β)
ただし,sinβ=a√a2+b2, cosβ=b√a2+b2
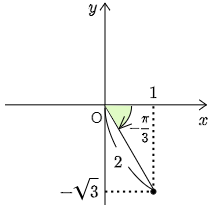
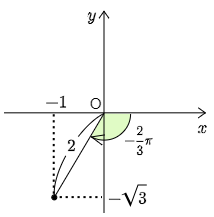
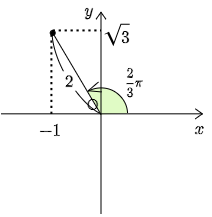
覚え方
座標平面上に,cos の係数を x 座標に,sin の係数を y 座標にもつ点 (b,a) をとり,原点Oと結ぶ.この線分の長さ(図の□)が合成したときの cos の係数であり,線分と x 軸の正の向きとのなす角(図の△)が合成したときに用いる角である.
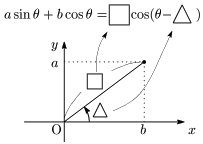
注意
sin での合成と異なり,cosでの合成では
√a2+b2cos(θ−β)
と cos の中身を「マイナス」にして,上図の△の角を引かなければならない.これは cos の合成公式が,cos の加法定理である
cosαcosβ+sinαsinβ=cos(α−β)
を根拠に導かれたことによっている.この式の右辺の「マイナス」がそれを指す.

例題 次の式を rcos(θ−α) の形に変形せよ.ただし,r>0,−π<α<π とする.
(1) −√3sinθ+cosθ
(2) −√3sinθ−cosθ
(3) √3sinθ−cosθ

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅱ 第4章 三角関数
| スライド | ノート | 問題 | |
| 1. 一般角と弧度法 | [会員] | ||
| 2. 一般角の三角関数 | [会員] | ||
| 3. 三角関数の性質 | [会員] | [会員] | |
| 4. 三角関数のグラフ | [会員] | ||
| 5. 三角関数の加法定理 | [会員] | [会員] | |
| 6. 三角関数の種々の公式 | [会員] | ||
| 7. 三角関数の合成 | [会員] | ||
| 8. 三角関数の応用 | [会員] |