座標平面の基礎｜内分・外分・2点間の距離・対称点・三角形の重心をスライドでやさしく解説

高校数学[総目次]

数学Ⅱ　第3章　図形と方程式

	スライド	ノート	問題
1. 座標平面上の点
2. 直線の方程式
3. 円の方程式
4. 円と直線
5. 軌跡と方程式
6. 不等式と領域

1．座標平面上の点

1.1　数直線上の点

　数直線上の1点をPとするとき，Pに対応する実数 $x$ をPの座標といい，$\mathrm{P}(x)$ で表す．例えば下の図では点Pが2に対応しているから $\mathrm{P}(2)$ と表す．

　数直線上に2点A，Bをとり，線分ABを考える．この線分を $m:n$ に分ける方法として，内分と外分を説明する．内分の方は特に問題ないだろうが，外分の方は少しわかりにくいので注意を要する．

　内分や外分の概念は，数直線上の線分に限らず，一般の線分に対して定義されるが，ここでは数直線上の線分に限定して話を進める．

内分点

　数直線上の2点A，Bについて，線分AB上に点Pがあるとする．このとき，$\mathrm{A}\mathrm{P}:\mathrm{P}\mathrm{B}=m:n$ であるならば，点Pは線分ABを $m:n$ に内分するといい，Pを内分点（ないぶんてん）という．

注意

　例えば $1:2$ に内分するといっても「線分ABを $1:2$ に内分する」というのと「線分BAを $1:2$ に内分する」というのは異なる．要するにAとBのどちらの点を先に述べるかということである．

　数直線上の2点 $\mathrm{A}(a)$，$\mathrm{B}(b)$ について，線分ABを $m:n$ に内分する点 $\mathrm{P}$ の座標 $x$ を求めてみよう．

1°　$a<b$ のとき

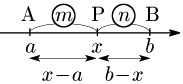
$$\begin{array}{rl}(x-a):(b-x)& =m:n\\ n(x-a)& =m(b-x)\\ (m+n)x& =na+mb\\ \therefore x& =\frac{na+mb}{m+n}\end{array}$$

2°　$a>b$ のとき

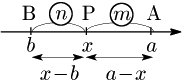
$$\begin{array}{rl}(a-x):(x-b)& =m:n\\ n(a-x)& =m(x-b)\\ (m+n)x& =na+mb\\ \therefore x& =\frac{na+mb}{m+n}\end{array}$$

　1°，2° ともに同じ結果となるから次が成り立つ：

内分点　数直線上の2点A$(a)$, B$(b)$について，線分ABを$m:n$に内分する点の座標は，$$\frac{na+mb}{m+n}$$　特に，線分ABの中点（$1:1$に内分する点）の座標は，$$\frac{a+b}{2}$$

例　　数直線上の2点 $\mathrm{A}(3)$，$\mathrm{B}(6)$ について，

(1) 線分ABを $2:1$ に内分する点の座標

$$\frac{1\times 3+2\times 6}{2+1}=5$$

(2) 線分ABの中点

$$\frac{3+6}{2}=\frac{9}{2}$$

外分点

　数直線上の2点A，Bについて，数直線上の線分ABの外側に点Qがあるとする．このとき，$\mathrm{A}\mathrm{Q}:\mathrm{Q}\mathrm{B}=m:n$ であるならば，点Qは線分ABを $m:n$ に外分するといい，Pを外分点（がいぶんてん）という．

　内分のときと違って外分は少し難しい．数直線上の2点A，Bをとって線分ABを考えるところまでは同じなのであるが，内分のときには点Pを線分AB上にとったのに対し，外分では数直線上の線分AB以外のところ，つまり外側にとるのである．

　外分を理解するために，「線分ABを $2:1$ に外分する点P」と「線分ABを $1:2$ に外分する点Q」の2つを例にとろう．ポイントは「ひと筆書き」である．

1°　線分ABを $2:1$ に外分する点P

　数直線上のAに鉛筆を置き，そこから数直線に沿って2だけ進んだところにPを書く．ただしPは線分ABの外側にとる．そして鉛筆を浮かすことなくそこから1だけ移動させるとBにたどり着く．そのような点Pが線分ABを $2:1$ に外分する点である．

2°　線分ABを $1:2$ に外分する点Q

　数直線上のAに鉛筆を置き，そこから数直線に沿って1だけ進んだところにQを書く．ただしQは線分ABの外側にとる．そして鉛筆を浮かすことなくそこから2だけ移動させるとBにたどり着く．そのような点Qが線分ABを $1:2$ に外分する点である．

　アニメーションの鉛筆の動きからわかるように，$m:n$ に外分するというときの外分点の位置は，$m>n$ ならばAからBに向かう側にあり，逆に $m<n$ ならばBから遠ざかる側にある．

　数直線上の2点 $\mathrm{A}(a)$，$\mathrm{B}(b)$ について，線分ABを $m:n$ に外分する点 $\mathrm{Q}$ の座標 $x$ を求めてみよう．

1°　$m>n$ のとき

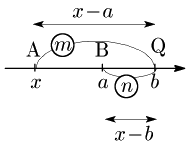
$$\begin{array}{rl}(x-a):(x-b)& =m:n\\ m(x-b)& =n(x-a)\\ (m-n)x& =-na+mb\\ \therefore x& =\frac{-na+mb}{m-n}\end{array}$$

2°　$m<n$ のとき

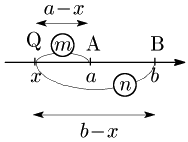
$$\begin{array}{rl}(a-x):(b-x)& =m:n\\ n(a-x)& =m(b-x)\\ (m-n)x& =-na+mb\\ \therefore x& =\frac{-na+mb}{m-n}\end{array}$$

　1°，2° ともに同じ結果となるから次が成り立つ：

外分点　数直線上の2点A$(a)$, B$(b)$について，線分ABを$m:n$に外分する点の座標は，($m$と$n$の大小関係によらず)$$\frac{-na+mb}{m-n}$$

例　　数直線上の2点 $\mathrm{A}(3)$，$\mathrm{B}(5)$ について，

(1) 線分ABを $2:1$ に外分する点の座標

$$\frac{-1\times 3+2\times 5}{2-1}=7$$

(2) 線分ABを $1:2$ に外分する点の座標

$$\frac{-2\times 3+1\times 5}{1-2}=1$$

1.2　座標平面上の点

2点間の距離

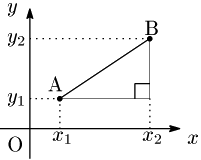
　2点 $\mathrm{A}(x_1,y_1)$，$\mathrm{B}(x_2,y_2)$ について，2点A，B間の距離ABは，三平方の定理により，

$${\mathrm{A}\mathrm{B}}^2=(x_2-x_1{)}^2+(y_2-y_1{)}^2$$

となる．この式は，ABが $x$ 軸に垂直な場合($x_1=x_2$)や，$y$ 軸に垂直な場合($y_1=y_2$)でも成り立つ．
　$\mathrm{A}\mathrm{B}>0$ であるから，

$$\mathrm{A}\mathrm{B}=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$$

　特に，点Bが原点 $\mathrm{O}(0,0)$ のとき，

$$\mathrm{O}\mathrm{A}=\sqrt{{x_1}^2+{y_1}^2}$$

2点間の距離　平面上の2点A$(x_1,y_1)$, B$(x_2,y_2)$について，2点間の距離ABは，$$\mathrm{A}\mathrm{B}=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2}$$　特に，Bが原点$(0,0)$のとき，$$\mathrm{O}\mathrm{A}=\sqrt{{x_1}^2+{y_1}^2}$$

例　　A$(1,4)$，B$(3,2)$ のとき，

$$\begin{array}{rl}\mathrm{A}\mathrm{B}& =\sqrt{(3-1{)}^2+(2-4{)}^2}\\ & =\sqrt{8}\\ & =\underset{―}{\mathbf{2}\sqrt{\mathbf{2}}}\end{array}$$

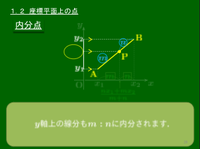
内分点・外分点

　平面上の2点 $\mathrm{A}(x_1,y_1)$，$\mathrm{B}(x_2,y_2)$ について

1° 線分ABを $m:n$ に内分する点P

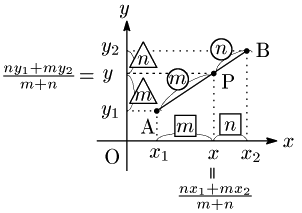
2° 線分ABを $m:n$ に外分する点Q

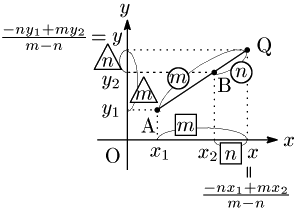
　平行線と線分の比の関係を考えると，結局数直線上の2点の場合に帰着される．

まとめ　平面上の2点A$(x_1,y_1)$, B$(x_2,y_2)$ について，線分ABを $m:n$ に$$\begin{array}{rl}& \text{内分する点}:(\frac{n{x}_1+m{x}_2}{m+n},\frac{n{y}_1+m{y}_2}{m+n})\\ & \text{特に中点は}(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\\ & \text{外分する点}:(\frac{-n{x}_1+m{x}_2}{m-n},\frac{-n{y}_1+m{y}_2}{m-n})\end{array}$$

例　平面上の2点 $\mathrm{A}(0,1)$，$\mathrm{B}(3,4)$ について

(1) $2:1$ に内分する点

$$(\frac{1\cdot 0+2\cdot 3}{2+1},\frac{1\cdot 1+2\cdot 4}{2+1})$$

$$\therefore (2,3)$$

(2) 中点

$$(\frac{0+3}{2},\frac{1+4}{2})$$

$$\therefore (\frac{3}{2},\frac{5}{2})$$

(3) $4:1$ に外分する点

$$(\frac{-1\cdot 0+4\cdot 3}{4-1},\frac{-1\cdot 1+4\cdot 4}{4-1})$$

$$\therefore (4,5)$$

(4) $1:4$ に外分する点

$$(\frac{-4\cdot 0+1\cdot 3}{1-4},\frac{-4\cdot 1+1\cdot 4}{1-4})$$

$$\therefore (-1,0)$$

対称な点

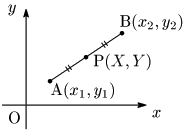
　2点A$(x_1,y_1)$，B$(x_2,y_2)$ が点P$(X,Y)$ に関して対称な位置にあるとき，

点Pは線分ABの中点

と捉える．

例題　点A$(1,4)$と，点P$(3,2)$に関して対称な点Bの座標は？

　点P$(3,2)$ は線分ABの中点だから，

$$\{\begin{array}{l}{\displaystyle \frac{1+x}{2}}=3\\ {\displaystyle \frac{4+y}{2}}=2\end{array}\therefore \{\begin{array}{l}x=5\\ y=0\end{array}$$

　よって，B$\mathbf{(}\mathbf{5}\mathbf{,}\mathbf{0}\mathbf{)}$

三角形の重心

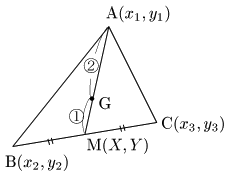
　辺BCの中点をM$(X,Y)$ とおくと，

$$\{\begin{array}{l}X={\displaystyle \frac{x_2+x_3}{2}}\\ Y={\displaystyle \frac{y_2+y_3}{2}}\end{array}$$

　重心Gは，線分AMを $2:1$ に内分する点であるから，G$(x,y)$ は，

$$\{\begin{array}{l}x={\displaystyle \frac{1\cdot x_1+2X}{2+1}}={\displaystyle \frac{x_1+x_2+x_3}{3}}\\ y={\displaystyle \frac{1\cdot y_1+2Y}{2+1}}={\displaystyle \frac{y_1+y_2+y_3}{3}}\end{array}$$

まとめ　3点A$(x_1,y_1)$, B$(x_2,y_2)$, C$(x_3,y_3)$について，△ABCの重心の座標は，$$(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})$$

---

高校数学[総目次]

数学Ⅱ　第3章　図形と方程式

	スライド	ノート	問題
1. 座標平面上の点
2. 直線の方程式
3. 円の方程式
4. 円と直線
5. 軌跡と方程式
6. 不等式と領域