整式の除法（筆算・組立除法）｜スライドで学ぶ高校数学

このページにある内容は，こちらのスライド でわかり易く説明しています．

PC環境なら全画面表示でより見やすく，よりわかりやすい！
全画面表示の仕方は こちら

数学Ⅱ　第1章　式と証明

	スライド	ノート	問題
1. 整式の除法
2. 分数式
3. 恒等式
4. 等式の証明
5. 不等式の証明

1. 整式の除法

　ここでは式を式で割る割り算を学習する．ここでいう式とは整式と呼ばれるもので，整式とは単項式または多項式のことを指す．

　単項式： $x, 5 x^{2}, \frac{1}{4}$ など
　多項式： $2 x + 3, x^{2} - 5 x + 1, x^{3} + 2 x$ など

以下において，整式の係数はすべて実数であるとする．

1.1　商と余り

式どうしの割り算とは何を意味するのか

　割り算といえば，例えば「7÷2＝3 余り 1」などが思い浮かぶ．それでは式どうしの割り算，例えば

$(x^{2} + 5 x + 10) \div (x + 2)$ 　　… (☆)

とは一体何を意味するのであろうか？ $x$ に特定の値を代入すれば $x^{2} + 5 x + 10$ も $x + 2$ も値が定まって割り算が実行できることもある．試しに $x = 1$ とおいてみると，

$1^{2} + 5 \cdot 1 + 10 = 16, 1 + 2 = 3$

となるから，16÷3＝5 余り 1 である．しかしこれから学ぼうとしている整式の除法ではこのような割り算を意味しない．実際，上の (☆) の割り算を行うと，余りは4となる．では式どうしの割り算とは一体何を意味し，どうすれば割り算が実行できるのであろうか？

式どうしの割り算は，掛け算から考える

　6÷2 の答えは3であるが，この商である3を

$6 = 2 \times □$

を満たす□であると考えることができる．式どうしの割り算というのは，実はこのように掛け算から考えるのである．例えば

$(x^{2} + 3 x + 2) \div (x + 1)$

という割り算を考えると，

$x^{2} + 3 x + 2 = (x + 1) \times \underset{―}{}$

というようにして　　　に入る式が何であるかを考えればよい．左辺を因数分解すればわかるように，

$x^{2} + 3 x + 2 = (x + 1) \times \underset{―}{(x + 2)}$

であるからこの割り算の商は $x + 2$ なのである．

　一般に，2つの整式 $A, B$ について，

$A = B Q \dots$ ①

となる整式 $Q$ が存在するとき，

$A$ は $B$ で割り切れる

といい， $Q$ を商という．

例

　 $x^{2} - 2 x - 3 = (x + 1) (x - 3)$
　よって， $x^{2} - 2 x - 3$ は $x + 1$ で割り切れ，そのときの商は $x - 3$ である．

式どうしの割り算でも割り切れない場合があり，その場合は余りがでる

　「7÷2＝3 余り 1」のように，整数の割り算では割り切れずに余りが出る場合がある．そして式どうしの割り算においても，割り切れないということが起こり得る．冒頭の例をもう一度使おう．

$(x^{2} + 5 x + 10) \div (x + 2)$ 　　… (☆)

　この割り算は

$x^{2} + 5 x + 10 = (x + 2) \times \underset{―}{}$

というようにして　　　に入る式を考えても，残念ながらそのような式は存在しない．そこで整数の割り算に立ち返って考えてみよう．

　「7÷2＝3 余り 1」から

$7 = 2 \times 3 + 1$

という関係が得られる．ここで余りである1は，割る数である2より小さい数でなくてはならないということには十分注意しておく必要がある．「7÷2＝2 余り 3」と書いてしまったときには「3はまだ2で割れますね」と小学校の先生に指導されたことであろう．実はこれと同じようなことが式どうしの割り算でも要請される．

　(☆)の割り算について，次の形にすることを考えてみよう：

$x^{2} + 5 x + 10 = (x + 2) \times {\underset{―}{}}_{(ア)} + {\underset{―}{}}_{(イ)}$

　このとき ${\underset{―}{}}_{(ア)}$ が商で， ${\underset{―}{}}_{(イ)}$ が余りとなるのである．ただし余りである ${\underset{―}{}}_{(イ)}$ に入る式は

(割る式の次数) ＞ (余りの式の次数)

となるように決める．(☆)の割り算の場合は，割る式 $x + 2$ の次数が1であるから余りの式の次数は0，すなわち定数である．このように整数の割り算での

(割る数) ＞ (余りの数)

という約束が，式どうしの割り算では式の次数の大小に置き換わるのである．すると，

$x^{2} + 5 x + 10 = (x + 2) \times {\underset{―}{(x + 3)}}_{(ア)} + {\underset{―}{4}}_{(イ)}$

というようにして ${\underset{―}{}}_{(ア)}$ と ${\underset{―}{}}_{(イ)}$ が決定される．従って(☆)の割り算の商は $x + 3$ ，余りは4となる．

　一般に，2つの整式 $A, B$ について，「 $A$ が $B$ で割り切れない」とは， $A = B Q$ を満たす $Q$ がないときで，このとき

$A = B Q + R$
ただし， $(B$ の次数) $> (R$ の次数)

を満たす $Q$ と $R$ が一意的に定まる．
　この $Q$ を $A$ を $B$ で割ったときの商， $R$ を余りという．

例

　 $2 x^{3} + x - 3 = (x^{2} + 2 x - 1) (2 x - 4) + 11 x - 7$
　よって， $2 x^{3} + x - 3$ を $x^{2} + 2 x - 1$ (2次式) で割ったときの商は， $2 x - 4$ ，余りは $11 x - 7$ (1次式)

1.2　筆算による整式の除法

式どうしの割り算においても商と余りを筆算によって求めることができる

　上の(☆)の割り算で，商が $x + 3$ ，余りが4と出たが，この商や余りはどのようにして求めることができるのであろうか．整数の割り算では筆算によって商と余りを求めることができたが，実は式どうしの割り算においても全く同様に筆算によって求めることができるのである．詳しいやり方はスライド 参照．

例

(1)　 $x^{3} - x^{2} + x - 2$ を $x - 2$ で割ったときの商と余り

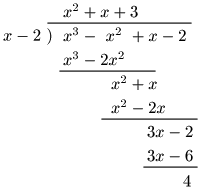
　　　よって，商 $x^{2} + x + 3$ ，余り $4$

(2)　 $2 x^{3} + x - 3$ を $x^{2} + 2 x - 1$ で割ったときの商と余り

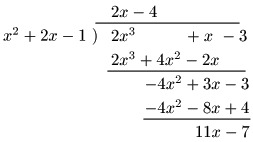
　　　よって，商 $2 x - 4$ ，余り $11 x - 7$

補足

　慣れてくれば，係数のみ書き出すのでよい．例えば上の(1)は次のようにする：

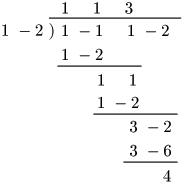
1.3　組立除法

　割る式が1次の式ならば，次の組立除法と呼ばれる計算方法もある．前節の例(1) $(x^{3} - x^{2} + x - 2) \div (x - 2)$ を組立除法によって計算すると次のようになる：

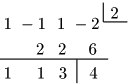
詳しいやり方はスライド 参照．

注意

　割る式の1次の係数が1でないときには注意を要する．

例　 $2 x^{3} - 5 x^{2} + 8 x + 2$ を $2 x - 1$ で割ったときの商と余り

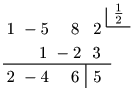
$\begin{aligned} 2 x^{3} - 5 x^{2} + 8 x + 2 & = (x - \frac{1}{2}) (2 x^{2} - 4 x + 6) + 5 \\ = (x - \frac{1}{2}) \cdot 2 (x^{2} - 2 x + 3) + 5 \\ = (2 x - 1) (x^{2} - 2 x + 3) + 5 \end{aligned}$

　　よって，商 $x^{2} - 2 x + 3$ ，余り $5$

このページで疑問は解決されましたか？

　こちら から数学に関するご質問・ご要望をお寄せください。

高校数学[総目次]