4. 反復試行の確率【ノート】
1人で学べる！高校数学

高校数学[総目次]

数学A　第2章　確率

	スライド	ノート
1. 事象と確率
2. 確率の基本性質
3. 独立な試行の確率
4. 反復試行の確率
5. 条件付き確率

4. 反復試行の確率

4.1　反復試行の確率

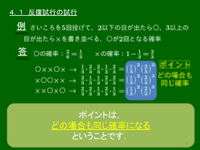
例　さいころを5回投げて，2以下の目が出たら〇，3以上の目が出たら×を書き並べる．〇が2回となる確率は？

　　　○となる確率：${\displaystyle \frac{2}{6}}={\displaystyle \frac{1}{3}}$
　　　×となる確率：$1-{\displaystyle \frac{1}{3}}={\displaystyle \frac{2}{3}}$

　○を2個，✕を3個の計5個を書き並べる．

　○✕✕○✕　→　${\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{2}{3}}\cdot {\displaystyle \frac{2}{3}}\cdot {\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{2}{3}}={\left({\displaystyle \frac{1}{3}}\right)}^2{\left({\displaystyle \frac{2}{3}}\right)}^3$

　✕○○✕✕　→　${\displaystyle \frac{2}{3}}\cdot {\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{2}{3}}\cdot {\displaystyle \frac{2}{3}}={\left({\displaystyle \frac{1}{3}}\right)}^2{\left({\displaystyle \frac{2}{3}}\right)}^3$

　✕✕○✕○　→　${\displaystyle \frac{2}{3}}\cdot {\displaystyle \frac{2}{3}}\cdot {\displaystyle \frac{1}{3}}\cdot {\displaystyle \frac{2}{3}}\cdot {\displaystyle \frac{1}{3}}={\left({\displaystyle \frac{1}{3}}\right)}^2{\left({\displaystyle \frac{2}{3}}\right)}^3$

ポイント　どの場合も同じ確率！

　結局 ${\left({\displaystyle \frac{1}{3}}\right)}^2{\left({\displaystyle \frac{2}{3}}\right)}^3$ という確率が，○2個と✕3個の順列の数，即ち

${}_5{\mathrm{C}}_2$

だけあるから，求める確率は

$${}_5{\mathrm{C}}_2{\left({\displaystyle \frac{1}{3}}\right)}^2{\left({\displaystyle \frac{2}{3}}\right)}^3=10\times \frac{2^3}{3^5}=\underset{―}{\frac{\mathbf{80}}{\mathbf{243}}}$$

　一般に次が成り立つ：

反復試行の確率　ある試行で事象 $A$ の起こる確率を $p$ とする．この試行を $n$ 回繰り返すとき，$A$ が $r$ 回起こる確率は， $${}_n\text{C}{}_r{p}^r(1-p{)}^{n-r}$$

---

高校数学[総目次]

数学A　第2章　確率

	スライド	ノート
1. 事象と確率
2. 確率の基本性質
3. 独立な試行の確率
4. 反復試行の確率
5. 条件付き確率