～解き始める前に～

答案の提出方法，注意点はこちら をご覧らんください。

１　次の計算をしなさい。

10点×4=40(点)

(1)　$2-\left(\dfrac13+\dfrac{5}{12}\right)$

(2)　13.6, 14, 16, 13, 12.4 の平均を求めなさい。

(3)　0.1÷0.002÷0.1

(4)　2時間4秒ー36分56秒

２　A，B，C，Dの4人が算数のテストを受けたところ，平均点は85点でした。試験当日に欠席していたEさんが，後日同じ試験を受けたところ，A～Eの5人の平均点は86点になりました。Eさんは何点でしたか。

10点

３　次の各問いに答えなさい。

10点×3=30(点)

(1)　3で割るとあまりが1となる2けた以上の整数のうち，小さい方から100番目の数を答えなさい。

(2)　5で割るとあまりが1となる2けたの整数は何個ありますか。

(3)　3で割っても5で割ってもあまりが1となる2けた以上の整数のうち，小さい方から100番目の数字を求めなさい。

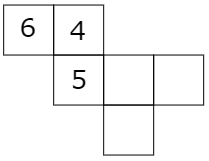
４　向かい合う面の数を足すと7になるさいころがあります。次の各問いに答えなさい。

10点×2=20(点)

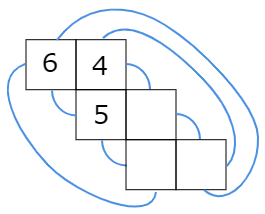
(1)　このさいころの展開図を完成させなさい。ただし，数字の向きは問いません。

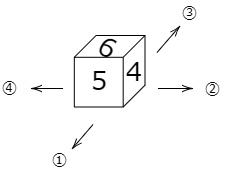
(2)　このさいころを図のように図のように置きます。ただし数字の向きは無視します。この状態のさいころを，①の方向に5回転がし，次に②の方向に3回転がし，次に③の方向に4回転がし，最後に④の方向に2回転がしました。このとき上の面の数字は何ですか。

　答案の提出