
1 次の計算をしなさい。
10点×4=40(点)
(1) $1-\left(\dfrac14+\dfrac{13}{28}\right)$
こたえ
カッコがあるときはカッコ内が優先(ゆうせん)です。
$\dfrac14+\dfrac{13}{28}=\dfrac7{28}+\dfrac{13}{28}=\dfrac{20}{28}=\dfrac57$
よって,$1-\dfrac57=\dfrac77-\dfrac57=\dfrac27$
答えは $\underline{\boldsymbol{\dfrac27}}$
(2) 47, 48, 49, 50, 51, 52, 53 の平均を求めなさい。
こたえ
一番小さな数である47を基準とすると
| 数 | 47 | 48 | 49 | 50 | 51 | 52 | 53 |
| 47との差 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
となりますから\[(0+1+2+3+4+5+6)\div7=21\div7=3\] よって 47+3=50
答えは 50
(3) 0.2÷0.001×0.3×0.4
こたえ
小数点の位置に気を付けましょう。
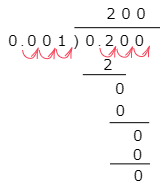
200×0.3=60
60×0.4=24
答えは 24
(4) 容積が1.8L(リットル)の水そうについて,底面のたてが12cm,横が0.05mでした。高さは何mmですか。ただし,水そうの厚みは考えません。
こたえ
1Lは1辺が10cmの立方体の体積です。10×10×10=1000ですから,1Lは1000cm3です。したがって1.8Lは1800cm3です。また,底面の横の長さは0.05mで,これは5cmです。よって底面の面積は\[12\times5=60{\rm cm}^2\]です。
60×□=1800 となる□は,1800÷60=30ですから30cm。単位をmmに直して,300mm。
答えは 300㎜
2 「99,95,35,18」は「あおもり」と読み,「98,09,66」を「いわて」と読む暗号があります。「85,97,68」は何と読みますか。
10点
こたえ
ひさしぶりのおしりたんてい暗号です。ぷぷっと解決してください。ヒントは50音表ですよ~。
「○△」の〇が子音(あ・か・さ・た・…)で,三角が母音(あ・い・う・え・お)です。各位の数を10から引くと,「あおもり」は「11,15,75,92」となり,「いわて」は「12,101,44」となります。よって下の50音表のように対応できます。

暗号の「85,97,68」は「25,13,42」で考えると「こうち(高知県)」です。
答えは こうち
3 次の各問いに答えなさい。
10点×3=30(点)
(1) 3で割るとあまりが1となる2けたの整数を,小さい方から5つ書きなさい。
こたえ
2けたの整数とは10から始まる数ですから順に3で割った余りを求めてみましょう。
10÷3=3あまり1 ○
11÷3=3あまり2 ×
12÷3=4 ×
13÷3=3あまり1 ○
14÷3=3あまり2 ×
15÷3=4 ×
16÷3=3あまり1 ○
17÷3=3あまり2 ×
18÷3=4 ×
$\vdots$
よって,10,13,16が「3で割るとあまりが1」となる整数ですね。小さい方から5個見つけなければならないので,あと2つ必要ですが,「10,13,16」という数字のならび方から,規則(きそく)を考えてみましょう。
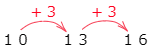
このように数字がならんでいますから,16の次の数字は16に3をたして19です。そしてその次も19に3を足して22です。
答えは 10,13,16,19,22
(2) 5で割るとあまりが1となる2けたの整数を,小さい方から5つ書きなさい。
こたえ
(1)と同じように10から順に5で割ったあまりを求めてみましょう。
10÷5=2あまり0 ×
11÷5=2あまり1 ○
12÷5=2あまり2 ×
13÷5=2あまり3 ×
14÷5=2あまり4 ×
15÷5=3あまり0 ×
16÷5=3あまり1 ○
17÷5=3あまり2 ×
$\vdots$
よって2桁の整数のうち,5で割るとあまりが1となる数は11,16,…となります。16-11=5です。実は5で割るとあまりが1となる数は「+5」をすると得られるのです。
16の次の数は 16+5=21
21の次の数は 21+5=26
26の次の数は 26+5=31
となります。これらはいずれも5で割るとあまりが1となります。
答えは 11,16,21,26,31
(3) 3で割っても5で割ってもあまりが1となる2けたの整数を小さい方から5つ書きなさい。
こたえ
(1)と(2)から,3で割っても5で割ってもあまりが1となる数字が1つは見つかりますね。問題は次の数字です。(2)の5つの数字で3で割ってあまりが1となる数字が他にないか探してください。
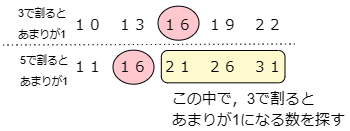
すると,31が3で割るとあまりが1となります。よっと3で割っても5で割ってもあまりが1となる数字は16,31,…となります。31の次の数字はというと,31-16=15により,31+15=46です。あとは15おきに現れます。
46の次の数は 46+15=61
61の次の数は 61+15=76
実はこの15という数字ですが,3と5の最小公倍数です。これは偶然(ぐうぜん)ではありません。こういった問題では常に成り立つことで,最初に16が見つかれば,あとは3と5の最小公倍数ごとに現れます。
答えは 16,31,46,61,76
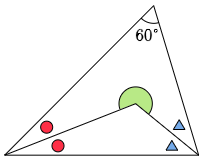
4 次の図において,赤色の○どうし,青色の△どうしは角の大きさが同じです。緑色の角の大きさを求めなさい。
10点×2=20(点)
(1)
こたえ
○と△の角の大きさを個別に求めようとしてもできませんが,○と△の合計の大きさなら計算できそうです。
○2個と△2個の角の大きさの合計は 180-60=120° です。
したがって,○1個と△1個の角の大きさの合計は 120÷2=60°
よって黄色の三角形の上の角は120° になります。
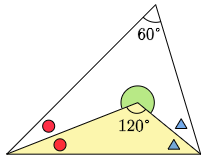
360-120=240°
答えは 240°
(2)
こたえ
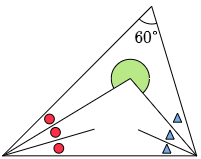
(1)と同様にして,○と△それぞれ2つ分の合計の大きさを求めてから計算しましょう。
○3個と△3個の角の大きさの合計は 180-60=120° です。
したがって,○1個と△1個の角の大きさの合計は 120÷3=40°
よって,○2個と△2個の角の大きさの合計は 40×2=80°
この結果,黄色の三角形の上の角は100° になります。
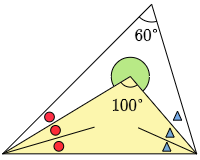
360-100=260°
答えは 260°

