~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) 1−(14+1328)
カッコがあるときはカッコ内が優先(ゆうせん)です。約分もお忘れなく。
(2) 47, 48, 49, 50, 51, 52, 53 の平均を求めなさい。
一番小さな数である47を基準とすると、下の表のようになりますから,0, 1, 2, 3, 4, 5, 6, 7の平均を求めて47を足せばよいのですね。
| 数 | 47 | 48 | 49 | 50 | 51 | 52 | 53 |
| 47との差 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
(3) 0.2÷0.001×0.3×0.4
(4) 容積が1.8L(リットル)の水そうについて,底面のたてが12cm,横が0.05mでした。高さは何mmですか。ただし,水そうの厚みは考えません。
2 「99,95,35,18」は「あおもり」と読み,「98,09,66」を「いわて」と読む暗号があります。「85,97,68」は何と読みますか。
10点
ひさしぶりのおしりたんてい暗号です。ぷぷっと解決してください。ヒントは50音表ですよ~。
3 次の各問いに答えなさい。
10点×3=30(点)
(1) 3で割るとあまりが1となる2けたの整数を,小さい方から5つ書きなさい。
5つ書いたあとに,これら5つの数字がどのような規則(きそく)でならんでいるか確認しておいてください。問題文に「2けたの整数」という条件があることにも注意しましょう。
(2) 5で割るとあまりが1となる2けたの整数を,小さい方から5つ書きなさい。
この問題でも,5つ書いたあとに,これら5つの数字がどのような規則(きそく)でならんでいるか確認しておいてください。問題文に「2けたの整数」という条件があることにも注意しましょう。
(3) 3で割っても5で割ってもあまりが1となる2けたの整数を小さい方から5つ書きなさい。
(1)と(2)から,3で割っても5で割ってもあまりが1となる数字が1つは見つかりますね。問題は次の数字です。(2)の5つの数字で3で割ってあまりが1となる数字が他にないか探してください。もし見つかったら,最初に見つけた数字との差はいくつになっていますか?実はこの問題でも(1)や(2)で現れた規則(きそく)と同じです。つまり差が一定になって現れるのです。
問題文に「2けたの整数」という条件があることにも注意しましょう。
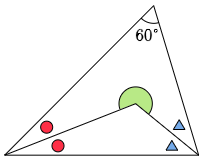
4 次の図において,赤色の○どうし,青色の△どうしは角の大きさが同じです。緑色の角の大きさを求めなさい。
10点×2=20(点)
(1)
○と△の角の大きさを個別に求めようとしてもできませんが,○と△の合計の大きさなら計算できそうです。
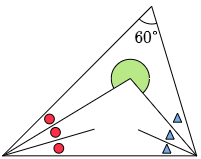
(2)
(1)と同様にして,○と△それぞれ2つ分の合計の大きさを求めてから計算しましょう。