6. (sin x)/xの極限(ノート)
スライドで学ぶ高校数学

高校数学[総目次]

数学Ⅲ　第1章　極限

	スライド	ノート
1. 数列の極限	[無料]
2. 無限等比数列	[無料]
3. 無限級数	[会員]
4. 無限等比級数	[会員]
5. 関数の極限	[会員]
6. (sin x)/x の極限	[会員]
7. 関数の連続性	[会員]

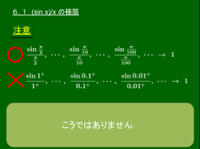
6.1 (sin x)/x の極限

重要 \[ \lim_{x\to 0}\frac {\sin x}x=1 \]

注意

　角度は弧度法(ラジアン)を用いる．

証明

　$x\to 0$ のときを考えるから，$0< |x| <\dfrac \pi 2$ としてよい．
[1]　$0<x<\dfrac \pi 2$ のとき

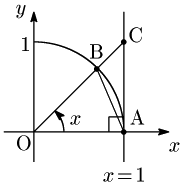
　図において， \[\begin{gather*} \mbox{△OAB}<\mbox{扇形OAB}<\mbox{△OAC}\\ \therefore\ \ \frac 12\cdot 1^2\sin x<\frac 12\cdot 1^2x<\frac 12\cdot 1\tan x\\ \therefore\ \ \sin x<x<\tan x \end{gather*}\] 　各辺を $\sin x(>0)$ で割ると， \[\begin{align*} &1<\frac x{\sin x}< \frac 1{\cos x}\\ \therefore\ \ &1>\frac{\sin x}x>\cos x\ \ \ (\mbox{逆数をとった}) \end{align*}\] 　$\displaystyle\lim_{x\to +0}\cos x=1$ であるから，はさみうちの原理により，$\displaystyle\lim_{x\to +0}\frac{\sin x}x=1.$

[2]　$-\dfrac\pi 2<x<0$ のとき
$x=-\theta$ とおくと，$x\to -0$ のとき $\theta\to +0$であるから， \[\begin{align*} \lim_{x\to -0}\frac{\sin x}x&=\lim_{\theta\to +0}\frac{\sin (-\theta)}{-\theta}\\ &=\lim_{\theta\to +0}\frac{\sin\theta}\theta=1. \ (\because [1]) \end{align*}\] 　[1]，[2] から $\displaystyle\lim_{x\to +0}\frac{\sin x}x=\lim_{x\to -0}\frac{\sin x}x=1$となるから， \[\lim_{x\to 0}\frac{\sin x}x=1.\]

■

補足

①　$x\to 0$ のとき，☆$\to 0$ ならば， \[ \lim_{x\to 0}\frac{\sin\mbox{☆}}{\mbox{☆}}=1 \] 　　例　$\displaystyle\lim_{x\to 0}\frac{\sin 5x}x=\lim_{x\to 0}\left(5\cdot\frac{\sin 5x}{5x}\right)=5\cdot 1=5.$
②　$\displaystyle\lim_{x\to 0}\frac 1{\frac{\sin x}x}=\frac 11=1$ により， \[ \lim_{x\to 0}\frac x{\sin x}=1. \] ③　三角関数と多項式が同時に含まれた式の極限をとるとき，簡単にその極限がわからない場合の多くで，この $\dfrac{\sin x}x$ の極限が一枚かんでいることが多い．

このページで疑問は解決されましたか？
　こちらから数学に関するご質問・ご要望をお寄せください。

---

高校数学[総目次]

数学Ⅲ　第1章　極限

	スライド	ノート
1. 数列の極限	[無料]
2. 無限等比数列	[無料]
3. 無限級数	[会員]
4. 無限等比級数	[会員]
5. 関数の極限	[会員]
6. (sin x)/x の極限	[会員]
7. 関数の連続性	[会員]