~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) 10116−114 (帯分数で)
16 から 14 は引けません。教科書では仮分数にしてから計算するように書かれていますが,整数全体を分数にする必要はありません。これまでと同様に必要なのは1だけですから,101を100+1にして1だけ 66 とします。つまり 10116 は 10076 です。10076−114 を考えましょう。
(2) 22.484÷2.8
(3) たて4cm,横6cm,高さ16cmの直方体を積み上げて立方体を作ります。立方体が最も小さくなるとき,直方体は何個使いましたか。
たては4の倍数,横は6の倍数,高さは16の倍数となります。立方体となるときの1辺の長さを求め,その長さとなるためにはたて,横,高さにそれぞれ何個ずつ並べたり,積んだりすればよいかを考えましょう。
(4) 1234秒は何分何秒ですか。
2 A市の人口は千の位までの概数(がいすう)で20000人です.A市の人口は何人以上,何人以下ですか.
10点
千の位までの概数ですから,百の位を四捨五入したのです。
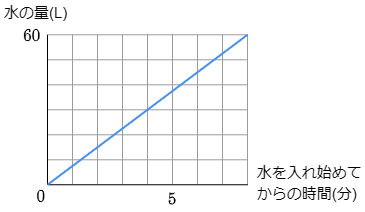
3 60L(リットル)入る直方体の形をした水槽(すいそう)に水を入れていきます。下のグラフはこの水槽に水を入れ始めてからの時間(分)と,水槽にたまった水の量(L)の関係を表しています。
次の各問いに答えなさい。
10点×3=30(点)
(1) 水槽には毎分何Lの水が入っていますか。
グラフから60L入るまでに何分かかったかを読み取りましょう。
(2) 水槽の底の面の面積が1500cm2のとき,水面の高さは1分間に何cmずつ上昇しますか。
この水槽の高さがわかれば1分間に水面が何cm上昇するかがわかります。まず,60Lは何cm3ですか?直方体の体積は(底面の面積)×高さですから,水槽の高さがここからわかります。
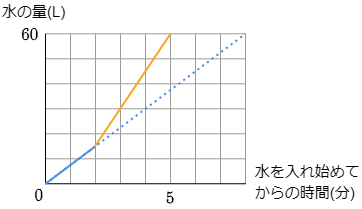
(3) 水槽に水を入れ始めてしばらくたってから,1分間に入れる水の量を増やしたところ,下のグラフのオレンジ色のようになりました。水の量を増やしたあとでは,毎分何Lの水が入っていますか。
1分間に入れる水の量を増やす直前までは水槽に何Lの水が入っていたでしょうか。それがわかれば残り何L入れることができるかがわかります。あとはそれを何分で入れたかをグラフから読み取りましょう。
4 次の角度を求めなさい。
10点×2=20(点)
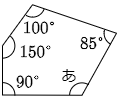
(1) 角度「あ」を求めなさい。
三角形の3つの角度の合計は180°ですが,五角形の5つの角度の合計は何度でしょうか?それには五角形に線を引いて,中に三角形をいくつか作ることでわかります。
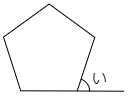
(2) 図は正五角形です。角度「い」を求めなさい。
正五角形は5つの角度の大きさがすべて等しい五角形です。(1)で五角形の5つの角度の合計は求めていますから,1つの角度の大きさが計算で求まります。角度「い」は,まっすぐな直線の角度が180°であることから求めることができます。