１ 次の計算をしなさい。
10点×4=40(点)
(1) $8\dfrac17-3\dfrac27+\dfrac17$ (帯分数で)
こたえ
$\dfrac17$ から $\dfrac27$ は引けませんから，8を7＋1にして1だけ $\dfrac77$ とします。$8\dfrac17=7\dfrac87$より\[7\dfrac87-3\dfrac27=4\dfrac67\] そして\[4\dfrac67+\dfrac17=4\dfrac77=5\] 答えは ５
別の考え方として，たし算と引き算は順番を変えることができます。そのときは引き算の「－」をすぐ後ろの数，この問題では $3\dfrac27$ にくっつけて，$-3\dfrac27$ として動かします。すると\[8\dfrac17+\dfrac17-3\dfrac27\]を計算すればよいのです。まず，$8\dfrac17+\dfrac17=8\dfrac27$ よって\[8\dfrac27-3\dfrac27=5\] 答えは ５
(2) 23.1÷0.15
こたえ
小数点の位置に気を付けましょう。
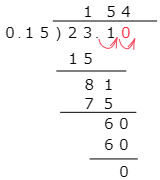
(3) たて30cm，横45cm，高さ60cmの直方体の中に立方体をぴったりつめます。できるだけ立方体の数を少なくするには，立方体の1辺を何cmにすればよいですか。
こたえ
30と45と60の3つの数の最大公約数を求めます。求め方は2つの場合と同じで，30の約数，45の約数，60の約数を書いていき，共通する約数の中で最も大きな数を探します。
30の約数：１,２,３,５,６,10, 15, 30
45の約数：１,３,５, 9, 15, 45
60の約数：１,２,３,4,5,6, 10,12,15, 30, …
よって最大公約数は15ですから，立方体の1辺の長さは15cmです。
答えは １５ｃｍ
(4) たて250cm，横520cmの長方形は何m2ですか。
こたえ
求める単位がm$^2$ですから，たてと横の単位をmになおしてから計算しましょう。
250cmは2.5m，520cmは5.2m。よって長方形の面積は\[2.5\times5.2=13\] 答えは １３ｍ２
２ 赤，白，青の3つの玉があります。百の位までの概数(がいすう)で，赤は100個，白は300個，青は900個ありました。赤，白，青の玉の合計は何個以上，何個以下ですか。
10点
こたえ
百の位までの概数ですから，十の位を四捨五入したのです。
赤：50個以上149個以下
白：250個以上349個以下
青：850個以上949個以下
50＋250＋850＝1150
149＋349＋949＝1447
答えは 1150個以上，1447個以下
３ あんりさんは，家を7時50分に出て歩いて900mはなれた学校に向かいましたが，出発して5分後に忘れ物に気がづいて走って取りに帰り，そしてすぐにまた急いで学校に向かいました。下のグラフはあんりさんの移動の様子を表したものです。
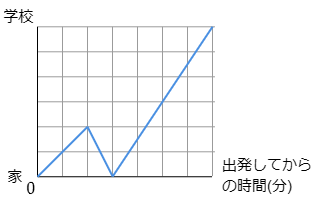
次の各問いに答えなさい。
10点×3=30(点)
(1) あんりさんが忘れ物に気がついたのは，家を出てから何mのところですか。グラフから判断して答えなさい。
こたえ
家から学校まで900mで，グラフではそれが縦軸(たてじく)の方向で表されています。縦軸方向は6めもりあります。従って1めもりは150mです。忘れ物に気が付いたのは縦軸方向に2めもりですから
150×2＝300
答えは 300m
(2) あんりさんが忘れ物に気がついてから家に帰るまでの間，1分間に何mの速さで走りましたか。
こたえ
グラフでは時間は横軸(よこじく)に表されています。あんりさんが忘れ物に気が付いたのは5分後で，グラフでは横軸の2めもり分です。従って1めもりは2分30秒を表しています。これは2.5分です。(1)から忘れ物に気が付いた地点は家から300mで，このきょりを2.5分で走ったのですから
300÷2.5＝120
答えは 1分間に120m
(3) あんりさんが家をふたたび出発してから忘れ物に気がついた地点まで戻(もど)ってきたとき，何時何分何秒でしたか。
こたえ
あんりさんが家からふたたび学校に向けて出発してから学校に到着するまでは，横軸に4めもり分の時間がかかっています。これは何分間かというと 2.5×4＝10(分間) です。
さらに家から忘れ物に気が付いた場所までは2めもり分で，これは家から学校までの6めもりに対して $\dfrac26$，約分して $\dfrac13$ です。6めもり分を10分間で移動したので，その $\dfrac13$ だけ移動するのにかかった時間は 10÷3ですが，割り切れないので別の考え方をしてみます。
10÷3＝3余り1なので，10から1を除いた9を3で割って3(分)。余りの1分ですが，1分は60秒ですから60÷3＝20(秒)
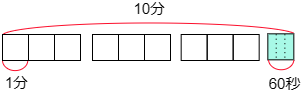
あんりさんがふたたび忘れ物に気が付いた地点に到着した時刻は
7時50分＋5分＋2分30秒＋3分20秒＝8時0分50秒
よって答えは 8時0分50秒
４ 次の図のように，正三角形１こから始めて，中に次々と小さな正三角形を増やしていき，図の中にある最も小さな正三角形の数を数えます。
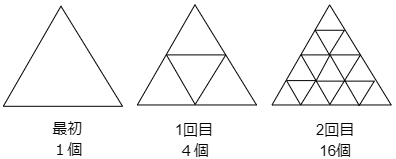
次の各問いに答えなさい。
10点×2=20(点)
(1) 4回目に増やしたとき，最も小さな正三角形は何個ありますか。
こたえ
最初と1回目を見てください。1個だった正三角形が4個に増えています。つまり1×4＝4(個)です。
次に1回目から2回目を見てください。下の図のように分けて考えると，1回目のときの変化と同じように，1個の正三角形が4個ずつに分かれています。1回目の後には4個ですから，このそれぞれが4個に分けられるのです。つまり，2回目のあとでは4×4＝16(個)です。
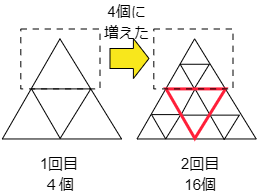
4個ずつの小さな正三角形になった。
つまり4×4＝16(個)
このように考えていくと
3回目：16×4＝64
4回目：64×4＝256
答えは 256個
(2) 4回目に増やしたとき，図のようにまず一番大きな正三角形の3つの頂点(ちょうてん)の部分に色をぬり，さらにとなりの正三角形どうしには色をぬらないように，ぬっていきました。色がぬられた正三角形は何個ですか。
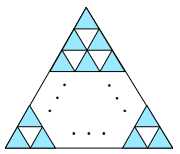
こたえ
色がついた正三角形の個数は，1段目には1個，2段目には2個，3段目には3個，…というようになっています。したがって4回目のあとに何段になっているかがわかれば求まりそうです。
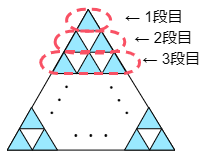
最初から1回目の変化では，1本の辺2つに分かれて2本になりますから，1×2＝2(段)です。
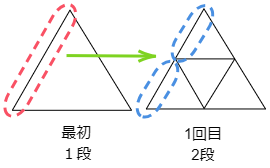
次に1回目から2回目の変化では，1回目のときと同じように，1つの正三角形の辺が2つに分かれています。したがって2×2＝4(段)になっています。
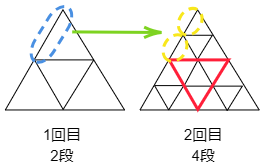
以下同じように4回目まで考えてみましょう。
3回目：4×2＝8
4回目：8×2＝16
したがって，4回目では16段になっていますから
1＋2＋3＋4＋…＋15＋16＝136
答えは 136個
