~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) 18−194(帯分数で答えなさい。)
まず 194 を帯分数にしましょう。そのあと18を17と1に分けて,1だけ分母を4とする分数にしましょう。
(2) 18.538÷2.3
(3) 172.5×0.87−172.5×0.77 (計算を工夫して求めなさい。)
計算の工夫をしてみましょう。分配の決まりを使うと計算がとてもラクになります。
(4) たて40cm,横1.1mの容器に水をいっぱいに入れると88L(リットル)入りました。この容器の高さは何cmですか。
1Lは1辺の長さが10cmの立方体の体積です。つまり10×10×10=1000(cm3)が 1L です。
容器の高さを□cmにして,□を使った式を作って考えましょう。
2 次の数字はある規則によって並べられています。100番目の数字は何ですか。
3, 6, 11, 18, 27, 38, 51, …
10点
以前にとても良く似た数字の並びを出題しています。思い出してください。ではもう少しヒントを出すと「-2」です。
3 ひまわりバス会社では,バスに乗る距離と運賃の関係を次のように定めています。
5kmまで 120円
10kmまで 160円
15kmまで 190円
20kmまで 240円
これについて次の各問いに答えなさい。
10点×3=30(点)
(1) 上の運賃表にもとづいて,下のグラフを完成させなさい。
例にならって続きを書きましょう。10kmから15kmと,15kmから20kmまでを横の線で書きます。
(2) バスと同じところを走る別の乗り物Aがあり,距離1kmにつき20円の割合で運賃が高くなっていきます。この乗り物Aの距離と運賃の関係を図に表すと1本の直線になります。それを(1)の図の中に書き入れなさい。
この乗り物Aは距離に応じて運賃が一定の割合で変化していきます。「割合」というのは容器に水を入れるときと同じで,例えば「1分間に2Lの割合で水を入れる」というのは1分後にいきなり0Lから2Lになるのではなく,少しずつ水がたまって1分後に2Lになりますね.これが「割合」の意味です。少しずつ変化していくという感じです。0kmではもちろん0円ですから,まずグラフの左下の部分を通ります。そして,例えば10kmのところの料金を計算してグラフ上に点を取り,先ほど取った左下の点と定規で結ぶと乗り物Aのグラフがかけます。
(3) バスと乗り物Aの距離と運賃の関係について,次の文を完成させなさい。
( )kmまでなら乗り物Aの方が運賃が安いが,それをこえるとバスの方が安くなる。
(1)と(2)でかいたグラフを見ると,どちらがどの場面で運賃が逆転するかがわかります。
4 次の各問いに答えなさい。
10点×2=20(点)
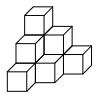
(1) 次の図は立方体を積み上げて作りました。立方体は全部で何個ありますか。
1段ずつスライスして考えます。
まず一番上の段は1個です。
2段目は3個です。
3段目は何個ですか?
これらをすべて足すと求める個数となります。
(2) (1)と同じような形を,10段まで積み上げました。立方体は全部で何個ありますか。
3段,4段,5段くらいまでなら何とか書いて考えることができますが,10段だとちょっと難しいですね。
実は立方体の個数にはある規則があるので,実際にかかなくても大丈夫なのです。
まず一番上の段が1個
次に上から2番目の段が3個ですから,1番上の段より2こ増えました。
そして上から3段目は6こですから2段目より3こ増えました。増えた個数の規則はどうなっているでしょうか?