高校数学[総目次]
数学Ⅱ 第3章 図形と方程式
| スライド | ノート | 問題 | |
| 1. 座標平面上の点 | |||
| 2. 直線の方程式 | |||
| 3. 円の方程式 | |||
| 4. 円と直線 | |||
| 5. 軌跡と方程式 | |||
| 6. 不等式と領域 |
演習問題
問題１【標準】
実数 a,b が a2+b2+a+b=1 を満たすとき，点 (a+b, ab) はどのような図形を描くか．
問題２【標準】
原点をOとする．直線 x+y=5 上を動点Pが動くとき，OP・OQ=20 を満たす半直線OP上の点Qの軌跡を求めよ．
問題３【標準】
点Pから放物線 y=x2 に引いた2本の接線が直交するとき，点Pの軌跡を求めよ．
問題４【発展】
xy 平面における2つの放物線 C:y=(x−a)2+b，D:y=−x2 を考える．
(1) C と D が異なる2点で交わり，その2交点の x 座標の差が1となるように実数 a, b が動くとき，C の頂点 (a, b) の軌跡を図示せよ．
(2) 実数 a, b が(1)の条件を満たしながら動くとき，C と D の2交点を結ぶ直線が通過する範囲を求め，図示せよ．
(東北大)
「軌跡とは何か．」これをひと言で表すと，「ある条件を満たす図形のことである」と言えるでしょう．例えば「1点からの距離が r である点の集合」という条件を満たす「軌跡」は「その点を中心とする半径 r の円」ということになりますし，「2点A，Bから等しい距離にある点の集合」という条件を満たす「軌跡」は「線分ABの垂直二等分線」ということになりましょう．このように与えられた条件を満たす図形が「軌跡」と呼ばれるものです．
では具体的にどのように軌跡を求めればよいのでしょうか．これには大きく2つあって，
① 条件から軌跡が簡単にわかるもの
② 条件から軌跡が簡単にわからないもの
に大別されます．①の方は，先述した円や垂直二等分線のようなものがその例です．そして数学として専ら問われるのは当然②の方で，これをどうやって求めていくかというところに難しさがあります．
その一つの手立てとして，条件を満たす点の座標を (x, y) とおいて，x と y の関係を調べるというのが極めて有効な手法です．例えば，与えられた条件を満たす x と y が y=2x+3 という関係を満たしていたとしましょう．するとそれは「傾きが2で y 切片が3である直線」という図形であることがわかります．y=x2 という関係を満たしているならば，それは放物線という図形であることがわかります．このように x と y の関係(方程式)がわかることで軌跡(図形)がわかるのです．
注意点として，得られた方程式が表す図形全体が求める軌跡であるとは限りません．いわゆる軌跡の限界と呼ばれるものですが，これについては軌跡の問題を考える上で常に気を付けておかなければなりません．
解答
{x=a+by=ab ⋯①
とおくと，条件式 a2+b2+a+b=1 は (a+b)2−2ab+(a+b)=1 と変形できますから
x2−2y+x=1
(∴y=12(x2+x−1) ⋯②)
と表せます．
（②の関係を満たすすべての点 (x,y) がOKではありません。例えば②上の点として (1,12) がありますが，①より a+b=1, ab=12 となり，この式を同時に満たす実数a,b は存在しません．実際，a,b は1±i2 で虚数です．よって②でOKとなる範囲を調べましょう。）
一方，①より a,b は解と係数の関係から t の2次方程式 t2−xt+y=0 ⋯③ の2解となりますから
a,b が実数 ⟺ ③の判別式 x2−4y≧0
②を代入して
x2−2(x2+x−1)≧0
x2+2x−2≦0
−1−√3≦x≦−1+√3
以上により求める軌跡は
放物線 x2−2y+x=1 の −1−√3≦x≦−1+√3 の部分 ⋯（答）
この問題でも軌跡の限界に気を付ける必要があります．
解答
P(X,Y)，Q(x,y)とおくと，P，Qは原点を通る同じ半直線上の点ですから
{X=txY=ty (t>0) ⋯①
とおけます．OP⋅OQ=20 より
√X2+Y2√x2+y2=t(x2+y2)=20
この式が成り立つとき x2+y2≠0 (即ち (x,y)≠(0,0) ⋯ ③)となりますから x2+y2 で割って
t=20x2+y2 ⋯②
また X,Y は x+y=5 上の点より X+Y=5．①を代入して
tx+ty=5 ∴ t(x+y)=5 ②を代入して 20x2+y2(x+y)=5
∴ (x−2)2+(y−2)2=8
従って③とから，求める軌跡は
円 (x−2)2+(y−2)2=8（ただし原点を除く） ⋯（答）
点Pの座標を (s, t) とするとき，Pを通る傾き m の直線が放物線と接する条件を求めます．s と t が定数であることに注意をすれば，その条件は m の2次方程式になります．つまり m の値として m1, m2 の2つが出てきます．あとは直交条件から傾きの積が −1 であることを利用して軌跡を求めます．
解答
P(s,t) とします．Pを通る傾き m の直線の方程式は
y−t=m(x−s)
∴y=mx−ms+t ⋯①
これが放物線 y=x2 と接するとき，mx−ms+t=x2，即ち2次方程式 x2−mx+ms−t=0 が重解をもちますから，判別式 D=0
D=m2−4(ms−t)=0
∴m2−4sm+4t=0 ⋯②
いま，②の2解を m1,m2 とすると，これらが接線①の傾きを表します．解と係数の関係から m1,m2=4t．よって直交条件より
m1m2=−1 ⟺4t=−1
∴t=−14
従って求める軌跡は 直線 y=−14 ⋯（答）
解答
(1) (x−a)2+b=−x2 より
2x2−2ax+a2+b=0 …①
C と D が異なる2点で交わるから，①の判別式を D とすると D>0 より
D/4=(−a)2–2(a2+b)>0
∴b<−a22 …②
また，①の2解を α, β とすると，解と係数の関係から α+β=a， αβ=a2+b2 であり，2交点の x 座標の差が1のとき， |α−β|=1 の両辺を2乗して (α−β)2=1 となるから (α+β)2−4αβ=1
故に a2−4⋅a2+b2=1
従って b=−a22−12 (これは②を満たす．)
よって求める軌跡は放物線 b=−a22−12
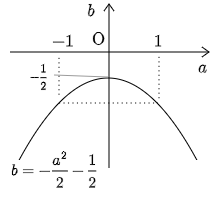
(2) [実数解条件に帰着する解法]
定数を k として
(x−a)2+b−y+k(x2+y)=0
は，C と D の交点を通る図形を表す．k=−1 とおくと
(x−a)2+b−y−(x2+y)=0
整理して 2ax+2y−a2−b=0
この方程式は直線を表すから，これが題意の直線である．(1)で得られた b=−a22−12 を代入して
2ax+2y−a2−(−a22−12)=0
整理して
a2−4xa−4y−1=0 …③
この直線が通過する領域を R とすると，
点 (X, Y)∈R
⟺a2−4Xa−4Y−1=0 を満たす実数 a が存在する．
⟺ 判別式 D/4=(−2X)2−(−4Y−1)≧0
⟺ Y≧−X2−14
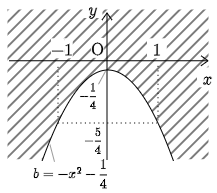
従って y≧−x2−14 で表される領域が求めるものである．ただし，境界線を含む．
別解１ [ファクシミリの原理による解法]
上の囲みの式③より y=14a2−xa−14
ここで x=X に固定し，右辺を a の関数とみて f(a) とおく．
平方完成して f(a)=14(a−2X)2−X2−14
(1)より a は実数全体をとり得るから，f(a) は a=2X で最小値 −X2−14 をとり，最大値はない．つまり固定した x=X に対して f(a) の値域は f(a)≧−X2−14 である．
ここで固定していた X を動かすと，求める領域は y≧−x2−14
(図は省略)
別解２ [包絡線による解法]
上の囲みの式③を a の関数とみて平方完成すると
(a−2x)2−4y−4x2−1=0 …④
よって直線③と曲線 −4y−4x2−1=0 即ち y=−x2−14 は x=a2 で接する．実際，③即ち④と −4y−4x2−1=0 を連立すると (a−2x)2=0 即ち (x−a2)2=0 となることから確かめられる．(図は省略)