7．2次方程式の解の配置【演習問題】｜スライドで学ぶ高校数学

Q: 判別式 D > 0 の条件は必要ないのですか．

必要ありません．$f(x)$ を平方完成したとき\[f(x)=(x-a)^2-a^2+3a\]となりますが，これを判別式 $D=a^2-3a$ を用いて表すと\[f(x)=(x-a)^2-D\]となります．$D>0$ というのは $f(x)$ の最小値 $-D$ が負であることと同値です．一方 $f(0)<0$ ということは，必ずしも最小値ではない $f(0)$ が負だというのですから，最小値である $-D$ は当然負です．よって\[-D<0\] 従って $D>0$ が自然と従います．わざわざ $D>0$ を課さなくてもよいのです．

Q: 判別式 D > 0 の条件は必要ないのですか．

必要ありません．$f(x)$ を平方完成したとき\[f(x)=(x-a)^2-a^2+3a\]となりますが，これを判別式 $D=a^2-3a$ を用いて表すと\[f(x)=(x-a)^2-D\]となります．$D>0$ というのは $f(x)$ の最小値 $-D$ が負であることと同値です．一方 $f(0)<0$ ということは，必ずしも最小値ではない $f(0)$ が負だというのですから，最小値である $-D$ は当然負です．よって\[-D<0\] 従って $D>0$ が自然と従います．わざわざ $D>0$ を課さなくてもよいのです．

高校数学[総目次]

数学Ⅰ　第1章　2次関数

	スライド	ノート	問題
1. 2次関数のグラフ	[無料]		[会員]
2. 関数のグラフの移動	[会員]		[会員]
3. 2次関数の最大・最小	[会員]		[会員]
4. 2次関数の決定	[会員]		[会員]
5. 2次関数のグラフと方程式	[会員]		[会員]
6. 2次不等式とグラフ	[会員]		[会員]
7. 2次方程式の解の配置	[会員]		[会員]

演習問題

　題材にした方程式は全問共通で，条件だけが少しずつ異なっています．さながら2次方程式の解の配置問題の博覧会といったところですが，ほんの些細な設定変更で難易度がぐっと変化するのは面白いところです．

問題１【基本】
　2次方程式 $x^2-2ax+3a-2=0$ の重解を含む2つの解が，ともに正となるような定数 $a$ の値の範囲を求めよ．

問題２【基本】
　2次方程式 $x^2-2ax+3a-2=0$ が， $0< x< 2$ の範囲に異なる2つの実数解をもつような定数 $a$ の値の範囲を求めよ．

問題３【基本】
　2次方程式 $x^2-2ax+3a-2=0$ が，正と負の解ををもつような定数 $a$ の値の範囲を求めよ．

問題４【標準】
　2次方程式 $x^2-2ax+3a-2=0$ が， $0< x < 2$ の範囲に解をもつような定数 $a$ の値の範囲を求めよ．

問題５【発展】
　2次方程式 $x^2-2ax+3a-2=0$ が， $0\leqq x \leqq 2$ の範囲に解をもつような定数 $a$ の値の範囲を求めよ．

問題６【発展】
　2次方程式 $x^2-2ax+3a-2=0$ が， $0\leqq x \leqq 2$ の範囲に解をもたないような定数 $a$ の値の範囲を求めよ．

問題１【基本】

　2次方程式 $x^2-2ax+3a-2=0$ の重解を含む2つの解が，ともに正となるような定数 $a$ の値の範囲を求めよ．

　　2次方程式の実数解は，2次関数のグラフと $x$ 軸との共有点の $x$ 座標に現れます．つまり，2次方程式の議論を2次関数の議論に持ち込むことによって，実数解を視覚的に捉えることができるようになるのです．この

「2次方程式」から「2次関数」へ

という理論の乗り入れが大切です．5．2次関数のグラフと方程式（演習問題) においては逆方向の

「2次関数」から「2次方程式」へ

があり，また 6．2次不等式とグラフ（演習問題) においては

2次不等式から2次関数へ，そして2次方程式へ

がありました．このように「2次関数」「2次方程式」「2次不等式」が三つ巴で相互に密接に関係しており，この3つの理論を相互に不自由なく行き来できるようになることが，この分野をストレスなく扱えるようになる最大のコツといってよいのかもしれません．

解答

　 $f(x)=x^2-2ax+3a-2=0$ とおきますと， $f(x)=(x-a)^2-a^2+3a-2$ から $f(x)$ のグラフの軸は直線 $x=a$ です．2次方程式 $x^2-2ax+3a-2=0$ すなわち $f(x)=0$ の実数解は， $f(x)$ のグラフと $x$ 軸との共有点の $x$ 座標に現れます．従って $f(x)$ のグラフの概形が次のようになればよいわけです．

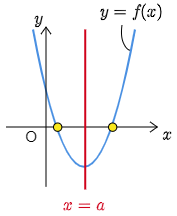
　誰もがこのようなグラフをかくためには次の3つの条件を課せばよいことがわかります：

　① $f(x)=0$ の判別式 $D$ は0以上
　② $f(x)$ のグラフの軸が $y$ より右側
　③ $f(0)$ の値が正

　これらをそれぞれ式で表すと

　① $D/4=a^2-1\cdot (3a-2)\geqq0$
　② $a>0$
　③ $f(0)=3a-2>0$

です．
　①を解くと， $(a-1)(a-2)\geqq0$ より $a\leqq 1,\ 2\leqq a$
　②はそのまま $a>0$
　③は $a>\dfrac23$
　これら3つの条件をすべて満たす $a$ の値の範囲が求めるもので，答えは　 $\dfrac23 < a\leqq 1$

問題２【基本】

　2次方程式 $x^2-2ax+3a-2=0$ が， $0< x< 2$ の範囲に異なる2つの実数解をもつような定数 $a$ の値の範囲を求めよ．

　問題の2次方程式は問題1のものと同じです．問題1の条件に加えて，今度は大きい方も2より小さくしなさいという条件が加わっています．ここでもグラフを用いて考えていきます．

解答

　条件を満たす $f(x)$ の概形は次のようになります．

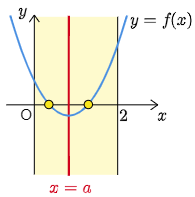
　誰もがこのようなグラフをかくためには次の4つの条件を課せばよいことがわかります：

　① $f(x)=0$ の判別式 $D$ は0以上
　② $f(x)$ のグラフの軸が $y$ より右側で直線 $x=2$ より左側
　③ $f(0)$ の値が正
　④ $f(2)$ の値が正

　これらはそれぞれ式で表すと

　① $D/4=a^2-1\cdot (3a-2)\geqq0$
　② $0<a<2$
　③ $f(0)=3a-2>0$
　④ $f(2)=2^2-4a+3a-2>0$

です．
　①を解くと， $(a-1)(a-2)\geqq0$ より $a\leqq 1,\ 2\leqq a$
　②はそのまま $0<a<2$
　③は $a>\dfrac23$
　④を解くと， $a<2$
　これら4つの条件をすべて満たす $a$ の値の範囲が求めるもので，答えは　 $\dfrac23 < a\leqq 1$

問題３【基本】

　2次方程式 $x^2-2ax+3a-2=0$ が，正と負の解ををもつような定数 $a$ の値の範囲を求めよ．

　条件を満たすような $f(x)$ のグラフは次のようになります．

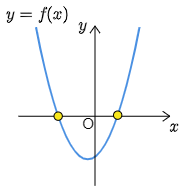
　誰もがこのようなグラフをかくための条件はどのようなものでしょうか．実はたった1つだけ条件を課しておけばよいのです．

解答

　求める条件は $f(0)<0$ すなわち $3a-2<0$ である．これを解いて答えは　 $a<\dfrac23$

よくある質問

判別式 D > 0 の条件は必要ないのですか．

　必要ありません． $f(x)$ を平方完成したとき $f(x)=(x-a)^2-a^2+3a$ となりますが，これを判別式 $D=a^2-3a$ を用いて表すと $f(x)=(x-a)^2-D$ となります． $D>0$ というのは $f(x)$ の最小値 $-D$ が負であることと同値です．一方 $f(0)<0$ ということは，必ずしも最小値ではない $f(0)$ が負だというのですから，最小値である $-D$ は当然負です．よって $-D<0$ 　従って $D>0$ が自然と従います．わざわざ $D>0$ を課さなくてもよいのです．　

問題４【標準】

　2次方程式 $x^2-2ax+3a-2=0$ が， $0< x < 2$ の範囲に解をもつような定数 $a$ の値の範囲を求めよ．

　問題2との違いに注意してください．「解にもつ」というのは「少なくとも1つ解をもつ」と言い換えます．2次方程式は最大2個の実数解をもちますから， $0< x < 2$ の範囲に重解も含めて2個の解を持つ場合と，ただ1つの解をもつ場合の2つが考えられ，それらを分けて考えます．