
1 次の計算をしなさい。
10点×4=40(点)
(1) $14\dfrac2{13}-4\dfrac7{13}$(帯分数で答えなさい。)
こたえ
$\dfrac2{13}$ から $\dfrac7{13}$ は引けませんから,14を13+1にし,$1\dfrac2{13}$ を仮分数にしてから計算しましょう.
$1\dfrac2{13}$ は $\dfrac{15}{13}$ です。
13-4=9, $\dfrac{15}{13}-\dfrac7{13}=\dfrac 8{13}$
答えは $9\dfrac 8{13}$
(2) $20\div0.05$
こたえ
小数点の位置に気をつけましょう。
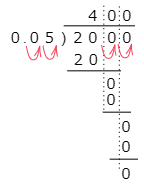
答えは 400
(3) $79.057\times0.21-79.057\times0.2$ (計算を工夫して求めなさい。)
こたえ
計算の工夫をしてみましょう。分配の決まりを使うと計算がとてもラクになります。
分配の決まりより
$79.057\times0.21-79.057\times0.2=79.057\times(0.21-0.2)$
0.21=0.2=0.01 ですから
$79.057\times0.01=0.79057$
答えは 0.79057
(4) 1辺が40cmの立方体の容器に水を高さが $\dfrac14$ のところまで入れました.この容器に入っている水の体積は何m3ですか。
こたえ
求める単位がm3ですから,長さの単位をmにしましょう。高さは40cmの $\dfrac14$ です。
40cm=0.4m です。高さは 40cm の $\dfrac14$ のところまで入っているのですから $40\times\dfrac14=10$ (cm)です。よって 0.1m。
よって水の体積は
0.4×0.4×0.1=0.016 (m3)
答えは 0.016m3
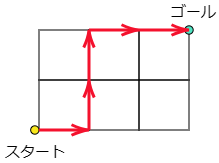
2 図において,スタートからゴールまで最短で行く方法は何通りありますか。
10点
こたえ
「もれなく,ダブりなく」数えましょう。
ちょっとうまい考え方を紹介しましょう。スタートからゴールまでの最短の道は↑2本と,→3本を一列に並べたもので表すことができます。例えば図の赤い矢印なら
→↑↑→→
という並べ方で表せます.すると求める最短で行く方法が何通りあるかは↑2本と,→3本の並べ方が全部で何通りあるかがわかればよいのです!
↑↑→→→
↑→↑→→
↑→→↑→
↑→→→↑
→↑↑→→
→↑→↑→
→↑→→↑
→→↑↑→
→→↑→↑
→→→↑↑
この10通りがそのまま答えとなります。
答えは 10通り
3 あいさんとみかさんの会話を読んで,次の問いに答えなさい。
あい「ねえ、1から9までの9つの数字の中でどれが一番好きかを当てる方法があるんだけど知ってる?」
みか「えー,知らない。教えて。」
あい「じゃあ,まずあなたの誕生日の日にちが1けたの数ならその数に9をかけてみて。誕生日が2けたの数なら,一の位と十の位を足した数に9をかけてみて。例えば1日なら1×9=9,2日なら2×9=18,12日なら1+2が3で,3×9=27という具合よ。」
みか「考えたわ。」
あい「その結果が1けたならそのままの数字を,もし2けたなら一の位と十の位を足したものを考えてみて。」
みか「考えたわ。」
あい「じゃあ,その数に1から9のうちあなたの好きな数字を足してみて」
みか「足したわ。」
あい「いくつになった?」
みか「13よ。」
あい「あなたの好きな数字がわかったわ。4ね。」
みか「すごい!どうしてわかったの?」
あい「実は最後に9をかけるというのがポイントなのよ。」
10点×3=30(点)
(1) みかさんの誕生日が23日で,好きな数字が4だとすると,最後に13になるまでのみかさんの途中の計算を説明しなさい。
こたえ
23日の23は2けたの数ですから,まずは十の位の数と一の位の数を足します。次のその数に9をかけます。その答えの一の位と十の位を足します。最後に4を足すと,13になります。
ステップ1 2+3=5
ステップ2 5×9=45
ステップ3 4+5=9
ステップ4 9+4=13
(2) あいさんの説明によれば,最後に9をかけるのがポイントだそうです。2から9までの8つの数字にそれぞれ9をかけて,その答えの一の位と十の位を足した数字はどうなるかすべて調べなさい。
こたえ
実際にかけ算を行って,一の位の数と十の位の数を足してみましょう。何かきそくが見つかるはずです。
2×9=18 → 1+8=9
3×9=27 → 2+7=9
4×9=36 → 3+6=9
5×9=45 → 4+5=9
6×9=54 → 5+4=9
7×9=63 → 6+3=9
8×9=72 → 7+2=9
9×9=81 → 8+1=9
(3) あいさんがみかさんの好きな数字を当てることができた理由を説明しなさい。
こたえ
(2)できそくがわかれば,あいさんがみかさんの好きな数字を当てられた理由がわかりますね。
1から9の各数字に9をかけると,1×9=9となり,2から9までは(2)で見たように,どんな場合でも十の位の数と一の位の数を足すと9になります。よって,みかさんが答えた13から9を引けば,みかさんの好きな数字がわかるというわけです。
4 次の各問いに答えなさい。
10点×2=20(点)
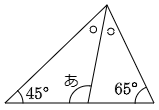
(1) 次の角度「あ」を求めなさい。ただし2つの○印どうしは角度が同じ大きさです。
こたえ
水色の三角形に注目すると,○2個分の角度の大きさは,45°+65°=110°ですから
180°-110°=70°
です。すると○1個分の角度の大きさは 70°÷2=35°です。
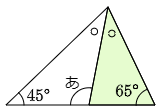
よって緑色の三角形に注目すると
あ=65°+35°=100°
答えは 100°
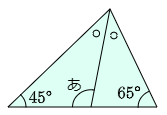
(2) 次の角度「い」を求めなさい。ただし2つの白い○印どうし,赤い○印どうしは角度が同じ大きさです。
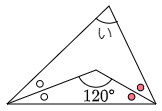
こたえ
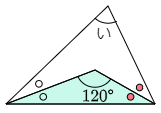
水色の三角形に注目すると,白色と赤色の○印の角の大きさを1個ずつ足したものは 180°-120°=60° です。すると,白色と赤色の○印の角の大きさを2個ずつ足したものは 60°×2=120° です。
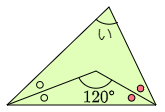
すると緑色の三角形に注目すると,
い=180°-120°=60°
答えは 60°

