高校数学[総目次]
数学A 第3章 図形の性質
| スライド | ノート | 問題 | |
| 1. チェバの定理 | |||
| 2. メネラウスの定理 | |||
| 3. チェバの定理の逆 | |||
| 4. メネラウスの定理の逆 | |||
| 5. 円に内接する四角形 | |||
| 6. 接弦定理とその逆 | |||
| 7. 方べきの定理とその逆 | |||
| 8. 三角形の五心 | |||
| 重心 | |||
| 外心 | |||
| 垂心 | |||
| 内心 | |||
| 傍心 |
中学校の範囲
| スライド | ノート | 問題 | |
| 1. 円周角の定理 | |||
| 2. 円周角の定理の逆 |

演習問題
問題1 [難易度 易]
△ABCにおいて,辺ABを 1:2 に内分する点をD,辺BCを 4:1 に外分する点をEとする.ACとDEの交点をPとするとき,AP:PC を求めよ.
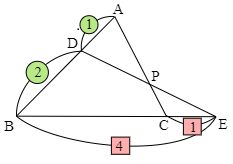
問題2 [難易度 標準]
△ABCにおいて,辺ABを 3:1 に外分する点をDとし,辺BCを 5:2 に外分する点をEとする.直線ACとDEの交点をPとするとき,AC:CP を求めよ.
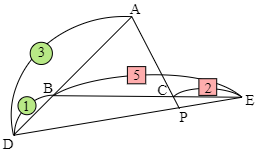
問題3 [難易度 やや難]
△ABCにおいて,辺ABの中点をD,辺BCを 3:2 に内分する点をEとし,AEとCDの交点をPとする.直線BPと辺ACとの交点をQとするとき,△PCQの面積は△ABCの面積の何倍か.
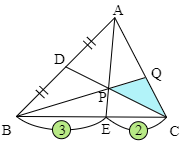
メネラウスの定理の式は辺の長さを用いた式になっていますが,例えば BQQC という部分は BQ:QC の比の値です.従って辺の長さそのものがわからなくても,比の値さえわかればよいという訳です. POINT
