高校数学[総目次]

数学Ⅰ　第2章　三角比

  スライド ノート 問題
1. 正接，正弦，余弦 [会員]   [会員]
2. 三角比の相互関係 [会員]   [会員]
3. 三角比の拡張 [会員]    
4. 正弦定理 [会員]   [会員]
5. 余弦定理 [会員]   [会員]
6. 三角形の面積 [会員]   [会員]

演習問題

問題１【基本】　　ヒント1　ヒント2
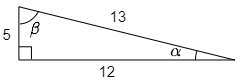
　次の図の直角三角形について，
　　tan⁡α, sin⁡α, cos⁡α，
　　tan⁡β, sin⁡β, cos⁡β
　の各値を求めよ．

問題２【基本】　　ヒント
　ある地点から高さ100mの塔の先端を見上げると，仰角が60°であった．その地点から塔の真下までの距離を求めよ．ただし，観測者の目の高さを1.5m，3=1.73として計算し，小数第2位を四捨五入せよ．

問題３【基本】　　ヒント
傾き30°の上り坂を40m進むと，水平方向に何m進み，鉛直方向に何m上がったことになるか．ただし，3=1.73として計算せよ．

問題４【基本】　　ヒント
半径 r の円Oにおいて，弧ABに対する中心角∠AOBの大きさが 2θ であるとき，弦ABの長さと，中心OからABに下ろした垂線OHの長さを，それぞれ r と θ を用いて表せ．

問題５【基本】　　ヒント
　半径10の円に内接する正方形の1辺の長さと，円の中心から1辺に下ろした垂線の長さをそれぞれ求めよ．

問題１【基本】

　次の図の直角三角形について，
　　tan⁡α, sin⁡α, cos⁡α，
　　tan⁡β, sin⁡β, cos⁡β
　の各値を求めよ．

　ヒント1　ヒント2

解答

　角 α の三角比を考えるときは，角 α を左下に移動させて考えます． POINT

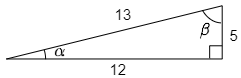
　図より

tan⁡α=512, sin⁡α=513, cos⁡α=1213

　同様にして，角 β の三角比を考えるときは，角 β を左下に移動させて考えます．