1 次の計算をしなさい。
10点×4=40(点)
(1) $14-\dfrac{72}{7}$
こたえ
$\dfrac{72}7=10\dfrac27=10+\dfrac27$ ですから,まず14を13と1に分けて,「13と1」から「10と $\dfrac27$」を引くことを考えます。
\[13-10=3\]
そして
\[1-\frac27=\frac57\]
よって答えは $\underline{\boldsymbol{3\dfrac57}}$
(2) $1\div16$ (答えは小数で)
こたえ
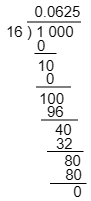
答えは 0.625
(3) $54\div6\div3\times2\div6\times4$
こたえ
わり算が2つ以上続くときは,前から割っていきます。
$54\div6=9$,$9\div3=3$
そして $3\times2=6$,$6\div6=1$,$1\times4=4$
答えは 4
(4) たて5cm,横5cm,高さが10cmの直方体の体積は何dLですか。
こたえ
この直方体の体積は,5×5で25,25×10で250(cm3)です。1dLは100cm3ですから,
\[250\div100=2.5\]
よって答えは 2.5dL
2 ある暗号は「15|22|51|101」を「おきなわ」と読み,「43|2314」を「つくえ」と読みます。では「45|24|12」は何と読みますか。
10点
こたえ
暗号の糸口は50音表です。

この表で,最初の数字の列と,あとの数字の行がクロスするところの文字があてはまります。
よって答えは とけい
3 上皿てんびんといくつかの重りがあります
次の問いに答えなさい。
10点×3=30(点)
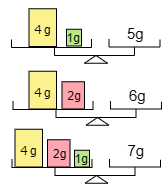
(1) 1g,2gの2つの重りと上皿てんびんを使ってはかることができる重さはいくつありますか。
こたえ
1gと2gがはかれるのは当然として,次のように両方乗せると3gがはかれますから,はかれるは1g,2g,3gの 3種類 です。
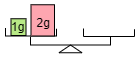
(2) 1g,2g,4gの3つの重りと上皿てんびんを使ってはかることができる重さはいくつありますか。
こたえ
(1)より1gと2gの2つの重りで1g,2g,3gがはかれることがわかりました。今度は4gもありますから,次のように乗せると5g,6g,7gがすべてはかれます。よって答えは 7種類
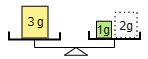
(3) 1g,3gの2つの重りと上皿てんびんを使ってはかることができる重さはいくつありますか。
こたえ
1gと3gと4gがはかれるのは当然として,次のように乗せると2gもはかることができます。よって答えは 4種類
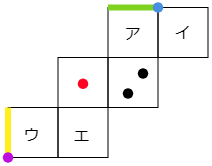
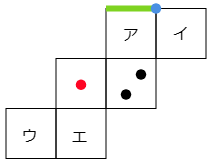
4 次はさいころの展開図です。
次の問いに答えなさい。
10点×2=20(点)
(1) 1の目がある面と平行な面はどれですか。また2の目がある面と平行な面はどれですか。それぞれア~エの中から答えなさい。
こたえ
組み立てたときに重なる辺どうしを線で結ぶと次のようになります。
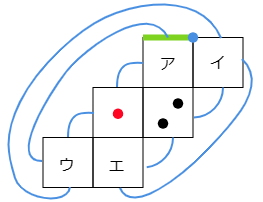
よって1の目がある面と平行な面は下の図より「イ」です。

また2の目がある面と平行な面も下の図から同じように考えると「ウ」です。
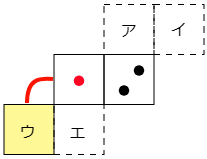
(2) 緑色の辺と重なる辺はどれですか。また青色の頂点と重なる部分はどこですか。それぞれ太線や黒丸で指し示しなさい。(展開図をノートに写して答えてください。)
こたえ
緑色の線が重なるように,展開図の一部をはさみで切って動かしてあげると下の図のようになります。
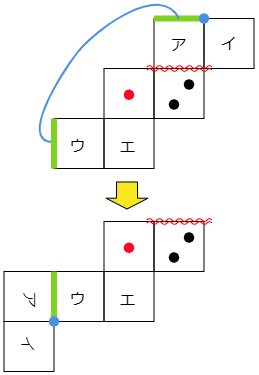
よって答えは下の図の黄色い線とむらさきの丸い点になります。