~解き始める前に~
答案の提出方法,注意点はこちら をご覧ください。
1 次の計算をしなさい。
10点×4=40(点)
(1) 123213−613
この問題は
123+213−613
と同じです。213−613 は計算できませんから,123213 を仮分数にするのですが,123を全部分数にする必要はありません。まずは123を書きかえて
122+1+213−613
としておきます。1は 1313 と同じですから
122+1313+213−613
というように1だけ仮分数にしてやりましょう。
(2) 3.56×2.3
最初は小数点を無視して 356×23 を計算します。計算できたら小数点を打ちます。小数点の位置に気を付けましょう。
(3) 17−(425+235−2×3)
もちろんカッコ内を先に計算します。カッコ内には足し算とかけ算が混ざっています。どちらが先でしたか?
(4) 1時間40分30秒+2時間35分54秒
1時間は60分ですから,60分のかたまりができたら1時間にくり上げます。同じように,1分は60秒ですから60秒のかたまりができたら1分にくり上げます。
2 次の数字はある規則に従って並んでいます。24番目の分数を答えなさい。
11, 12, 21, 13, 22, 31, 14, 23, 32, 41, 15, ⋯
10点
分子だけを見ていくと
1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 1, ⋯
となっています。次に分母だけ見ていくと
1, 2, 1, 3, 2, 1, 4, 3, 2, 1, 5, ⋯
となっています。すると問題に与えられたの分数たちは,
11 | 12,21 | 13,22,31 | 14,⋯
というようにグループに分けることができます。各グループにはいくつ分数が入っていますか?
1こ,2こ,3こ,4こ,⋯
となっていますね。すると例えば4つ目までのグループには
1+2+3+4=10(こ)
の分数があることがわかります。5つ目までのグループでは
1+2+3+4+5=15(こ)
6つ目までのグループでは
1+2+3+4+5+6=21(こ)
7つ目までのグループでは
1+2+3+4+5+6++7=28(こ)
という具合になっています。ということは24番目の分数はこの7番目のグループに入っていることがわかります。
ついでにグループ内では分子と分母を足した数が一定です。気がつきましたか?
3 1辺の長さが3cmの正方形の折り紙Aと,たて3cm,横6cmの長方形のおり紙Bがたくさんあります。
次の問いに答えなさい。
10点×3=30(点)
(1) たて12cm,横15cmの長方形の画用紙があります。この上には折り紙AとBをすきまなく,はみ出すことなく並べます。折り紙を最も多く使う場合と,最も少なく使う場合とでは何枚ちがいますか。ただし,折り紙Aと折り紙Bのどちらか一方だけを用いてもよいとします。
最も多く使う場合というのはもちろん折り紙Aだけを使う場合です。そして最も少ない場合というのはできるだけ多く折り紙Bを使う場合です。
(2) たて9cm,横15cmの長方形の画用紙があります。この上には折り紙AとBをすきまなく,はみ出すことなく並べます。折り紙を最も多く使う場合と,最も少なく使う場合とでは何枚ちがいますか。ただし,折り紙Aと折り紙Bのどちらか一方だけを用いてもよいとします。
最も多く使う場合は(1)と同様に折り紙Aだけを使う場合です。そして最も少ない場合も(1)と同じで,できるだけ多く折り紙Bを使う場合です。
(3) 折り紙AとBを自由に4枚使って長方形を作ります。何種類の長方形が作れますか。ただし,並べ方が違っていても,同じ形の長方形になるときは,それらを区別せずに1通りとして数えます。また,回転させると同じになるものも区別しません。
折り紙Aと折り紙Bの使う枚数の組合せは
の5通りです。それぞれの組み合わせからどのような長方形が何種類作れるでしょうか。
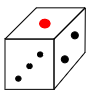
4 図のようなさいころがあります。このさいころは向かい合う面の目の数を足すと常に7になります。
次の問いに答えなさい。
10点×2=20(点)
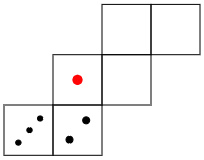
(1) 次の図は上のさいころの展開図です。残った面の目の数を書きなさい。ただし,「4,5,6」といったように数字で書きなさい。
あまり見たことのない展開図かもしれませんが,この形を切っており曲げるとちゃんと立方体になります。しかし見慣れた展開図にくらべて頭の中で組み立てるのが大変ですね。そんなとき,うまい考え方があります。
さいころの展開図では,くっつく辺どうしがはっきりしていれば,その2つの辺がくっつくように,展開図を移動させてもよいのです。例えば次のようにです。
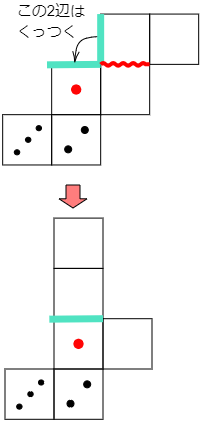
これなら最初の図よりずっと考えやすいですよね!
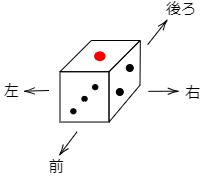
(2) さいころが図のようにおいてあります。前に5回転がしたあと,右に7回転がすとき,上の面にきている目の数は何ですか。「1,2,3,4,5,6」の数字で答えなさい。ただし,90∘ 回転させるごとに1回と数えることにします。
さいころを同じ方向に4回転がすと,元の状態に戻ります。ここがポイントです!つまり,同じ方向に4回転がすのは,転がさないのと同じなのです。
そしてもうひとつ。ある方向に3回転がすのはそれとは逆の方向に1回転がすのと同じです。3回も転がすのは大変ですが,1回転がすだけなら頭の中でイメージしやすいですよね!