
1 次の計算をしなさい。
(1) $5\dfrac27-2\dfrac47$
こたえ
5を $4+1$ にして,この1を $\dfrac77$ にすると,
\[5\dfrac27=4+1+\dfrac27=4\dfrac97\]
となります。よって
\[\begin{align*} 5\dfrac27-2\dfrac47&=4\frac97-2\frac47\\[5pt] &=(4-2)+\left(\frac97-\frac47\right)\\[5pt] &=2+\frac{9-4}7=\underline{\boldsymbol{2\frac57}} \end{align*}\]
(2) $2.74\times 14$
こたえ
$274\times14$ を筆算で計算すると

となります。小数点の位置を考えると答えは 38.36 です。
(3) $63-(24\div6\div3)\times3$
こたえ
$24\div6\div2$ から計算します。この計算は
\[(24\div6)\div2=4\div2=2\]
です。$24\div(8\div2)$ は間違いです。実際,
\[24\div(8\div2)=24\div4=6\]
となって,2になりません。よって答えは
\[63-2\times3=63-6=\underline{\boldsymbol{57}}\]
(4) $64\div8\div4\div2$
こたえ
(3)と同じで前から順に計算していきます。
\[\begin{align*} 64\div8&=8\\[5pt] 8\div4&=2\\[5pt] 2\div2&=\underline{\boldsymbol{1}} \end{align*}\]
2 ある都市の人口を四捨五入して千の位までの概数で表すと約13000人でした。この都市の人口として考えられるのは何人以上何人以下ですか。
こたえ
四捨五入して千の位が3ですから,答えは
12500人以上13500人未満
です。またここでは「人数」が問題になっていますから,答えが小数になることはありません。よって
12500人以上13499人以下
と答えてもよいでしょう。
3 たて15m,横20mの土地に花だんを作ります。花だんの周りには,幅が一定の通路を作ります。
次の問いに答えなさい。
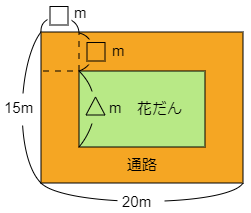
(1) 通路の幅を2mにすると,通路の面積は何m2ですか。
こたえ
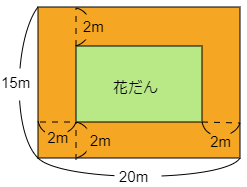
土地の面積は $15\times20=300({\rm m}^2)$ です。通路の幅が2mのとき,花だんのたての長さは
\[15-(2+2)=11(\rm m)\]
花だんの横の長さは
\[20-(2+2)=16(\rm m)\]
よって花だんの面積は
\[11\times16=176({\rm m}^2)\]
従って求める通路の面積は、土地全体の面積から花だんの面積を引いて
\[300-176=\underline{\boldsymbol{124({\rm m}^2)}}\]
[別の考え方]
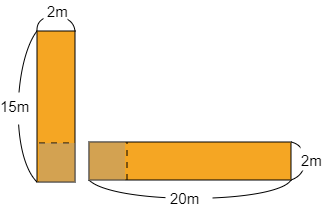
このような長方形の面積を2個ずつ足すと,四隅が2回足されています。ここに注意します。まず,左側の長方形の面積は
\[15\times2=30({\rm m}^2)\]
右側の長方形の面積は
\[2\times20=40({\rm m}^2)\]
よって,これらを2個ずつ足すと
\[30\times2+40\times2=60+80=140({\rm m}^2)\]
また,四隅の正方形の面積は
\[2\times2=4({\rm m}^2)\]
これが4個ありますから
\[4\times4=16({\rm m}^2)\]
よって求める通路の面積は,
$140-16=$124m2
[さらに別の考え方]
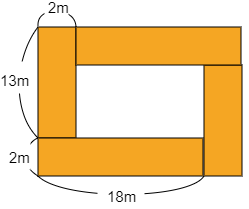
図のような,たて $15-2=13$(m),横2m の長方形2個の面積は
\[(13\times2)\times2=26\times2=52({\rm m}^2)\]
また,たて 2m,横 $20-2=18$(m) の長方形2個の面積は
\[(2\times18)\times2=36\times2=72({\rm m}^2)\]
従って求める通路の面積は、
\[52+72=\underline{\boldsymbol{124({\rm m}^2)}}\]
(2) 通路の幅を□m,花だんのたての長さを△mとすると,□と△の関係を式に表しなさい。
こたえ
通路2つ分と,花だんのたての長さの合計が,土地のたての長さが15mですから
□+□+△=15(m)
[別の考え方]
土地のたての長さから,通路2つ分を引くと花だんのたての長さが得られますから,
15ー(□+□)=△(m)
(3) 花だんのたてと横の長さの合計が23mのとき,通路の幅の長さを求めなさい。
こたえ
通路がなければ花だんのたてと横の合計は $15+20=35({\rm m})$ です。問題では花だんのたてと横の合計は23mですから,$35-23=12$(m) だけ減らさなければなりません。通路の幅が1m増えると花だんのたてと横の合計は4m減りますから,12m減らすためには通路の幅を $12\div4=$3(m) にすればよいのです。
4 1冊130円のノートを4冊と,1個30円のグミを何個か買って1000円を払うとおつりが270円でした。
次の問いに答えなさい。
(1) グミを何個買いましたか。
こたえ
1000円払っておつりが270円ですから、実際に支払った金額は
$1000-270=730$(円)
です。また,ノート4冊の代金は
$130\times4=520$(円)
です。よってグミに支払った代金は
$730-520=210$(円)
です。グミは1個30円ですから求める個数は
$210\div30=$7(個)
(2) 残ったおつりで1個20円のガムと1個15円のあめをあわせて16個買って,お金を使い切りました。ガムとあめはそれぞれ何個ずつ買いましたか。
こたえ
16個全部をガムにしたとすれば
$20\times15=300$(円)
です。しかしこれではおつりで残っている270円をオーバーしてしまいます。いくらオーバーしているかと言えば
$300-270=30$(円)
です。ですから15個すべてをガムにするのではなく,そこからいくつか減らし,減らした分をあめにしなければなりません。ガムとあめの価格差は $20-15=5$(円)ですから,1つガムをやめてあめに変えると代金が5円安くなります。従って30円安くするために,何個ガムからあめにかえなければならないかというと
$30\div5=6$(個)
です。15個のうち,あめを6個買うのですからガムは
$15-6=9$(個)
です。よって求めるものは
ガム9個,あめ6個
です。実際に確かめてみると,ガムの分は $20\times9=180$(円),あめの分は $15\times6=90$(円)。よって合計で $180+90=270$(円)となって問題に適しています。

