このページにある内容は,こちらのスライド(会員向け)でわかり易く説明しています.
高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | |
| 1. 不定積分 | [無料] | |
| 2. 置換積分法(不定積分) | [無料] | |
| 3. 部分積分法(不定積分) | [無料] | |
| 4. 定積分とその性質 | [会員] | |
| 5. 置換積分法(定積分) | [会員] | |
| 6. 部分積分法(定積分) | [会員] | |
| 7. 定積分と微分法 | [会員] | |
| 8. 定積分と和の極限 | [会員] | |
| 9. 定積分と不等式 | [会員] | |
| 10. 定積分の応用(面積) | [会員] | |
| 11. 定積分の応用(体積) | [会員] | |
| 12. 定積分の応用(回転体の体積) | [会員] | |
| 13. 曲線の長さ |
8.定積分と和の極限
8.1 区分求積法
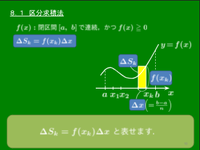
関数 $f(x)$ は区間 $[a,b]$ で連続,かつ $f(x)\geqq 0$ とする.この区間を $n$ 等分して,その分点を順に \[x_0(=a),x_1,x_2,\cdots ,x_n(=b)\] とおき,各区間の幅を $\Delta x\left(=\dfrac{b-a}n\right)$ とおく.曲線 $y=f(x)$ と $x$ 軸,及び2直線 $x=x_{k-1},x=x_k\ (k=1,2,\cdots,n)$ とで囲まれる部分の面積は,次の長方形領域の面積 $\Delta S_k$ で近似される: \[\Delta S_k=f(x_k)\Delta x\] よって曲線 $y=f(x)$ と $x$ 軸,及び2直線 $x=a,x=b$ で囲まれる部分の面積 $S$ は,次の①式で近似される: \[S\fallingdotseq\sum_{k=1}^n\Delta S_k=\sum_{k=1}^nf(x_k)\Delta x\ \ \cdots\mbox{①}\] ここで $n\to\infty$ として分割をどんどん細かくしていく$(\Delta x\to 0)$と,(①の誤差)$\to 0$ となるであろう.即ち \[S=\lim_{n\to\infty}\sum_{k=1}^nf(x_k)\Delta x\] となる.$S=\displaystyle\int_a^b\!\!f(x)\,dx$ であったから次が成り立つ:
\[ \lim_{n\to\infty}\sum_{k=1}^n f(x_k)\Delta x=\int_a^b\!\!f(x)dx \]
補足1
上の囲みの式を,和をとる番号を $k=0$ からにして, \[\lim_{n\to\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x=\int_a^b\!\!f(x)\,dx\] としてもよい.
補足2
特に $a=0$ のとき, \[x_k=\frac bnk,\ \ \Delta x=\frac bn\] であるから,
定積分と和の極限の公式(Ⅰ) \[\lim_{n\to\infty}\sum_{k=1}^n\frac bnf\left(\frac{kb}n\right)=\int_0^b\!\!f(x)\,dx\]
更に $b=1$ のとき,
定積分と和の極限の公式(Ⅱ)\[\lim_{n\to\infty}\sum_{k=1}^n\frac 1n f\left(\frac kn \right)=\int_0^1\!\!f(x)\,dx\]

8.2 いくつかの例題
例題1 次の極限を求めよ. \[\lim_{n\to\infty}\sum_{k=1}^n\frac\pi n\sin\frac{k\pi}n\ \ \cdots\mbox{①}\]
このような問題を見ると,数列で学習したいくつかの公式を利用して $\displaystyle \sum$ を具体的に計算してから極限をとりたくなる.実際その方法でも求められる問題もあるのだが,和をとることが困難な場合も多い.$\lim$ と $\displaystyle\sum$ が同時に登場している問題では区分求積法の利用をすぐに思いつけるようにしておきたい.次のイラストで印象付けておこう.

やり方その1 [ 公式(Ⅰ)に帰着させる ]
\[\begin{align*}
&\lim_{n\to\infty}\sum_{k=1}^n\frac \pi n\sin\frac{k\pi}n\hspace{6mm}\cdots\mbox{①}\\
&\lim_{n\to\infty}\sum_{k=1}^n\frac bnf\left(\frac{kb}n\right)\ \ \cdots\mbox{公式(Ⅰ)}
\end{align*}\]
①式と公式(Ⅰ)を比較すると, \[b=\pi,\ \ f(x)=\sin x\] であるから, \[\begin{align*} \mbox{①}&=\int_0^\pi\!\!\sin x\,dx\\ &=\Bigl[-\cos x\Bigr]_0^\pi\\ &=\underline{2} \end{align*}\]
やり方その2 [ 公式(Ⅱ)に帰着させる ]
ステップ1 $\dfrac1n$ を作る.
\[\mbox{①}=\lim_{n\to\infty}\sum_{k=1}^n\frac1n\cdot\pi\sin\left(\frac{k\pi}n\right)\]
ステップ2 $\dfrac kn$ を作る.
\[\mbox{①}=\lim_{n\to\infty}\sum_{k=1}^n\frac1n\cdot\pi\sin\left(\pi\times\frac kn\right)\]
ステップ3 $f(x)$ を決定する.($\dfrac kn$ を $x$ に置き換え)
\[f(x)=\pi\sin \pi x\]
以上により,
\[\mbox{①}=\int_0^1\!\!\pi\sin\pi x\,dx=\Bigl[-\cos \pi x\Bigr]_0^1=\underline{2}\]
例題2 次の極限を求めよ. \[\lim_{n\to\infty}\left(\frac1{n+1}+\frac1{n+2}+\cdots+\frac1{2n}\right)\ \ \cdots\mbox{①}\]
\[\begin{align*} \mbox{①}&=\lim_{n\to\infty}\sum_{k=1}^n\frac1{n+k}\ \ \leftarrow\ \sum\mbox{で表す}\\ &=\lim_{n\to\infty}\sum_{k=1}^n\frac1n\cdot\frac n{n+k}\ \ \leftarrow\ \frac 1n\mbox{を作る(ステップ1)}\\ &=\lim_{n\to\infty}\sum_{k=1}^n\frac1n\cdot\frac 1{1+\frac kn}\ \ \leftarrow\ \frac kn\mbox{を作る(ステップ2)}\\ &=\int_0^1\!\!\frac{dx}{1+x}\hspace{17mm} \leftarrow\ f(x)\mbox{の決定(ステップ3)}\\ &=\Bigl[\log(1+x)\Bigr]_0^1 \hspace{10mm} (\because\mbox{公式(Ⅱ))}\\ &=\underline{\log 2} \end{align*}\]
例題2の別解
$\displaystyle\sum_{k=1}^n\dfrac1{n+k}$ を次のような長方形の面積の総和として捉える:
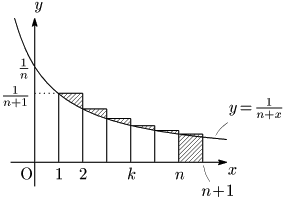
これらの長方形全体のうち,斜線部分の面積を $s_n$ とすれば,
\[\begin{align*} \sum_{k=1}^n\frac1{n+k}&=\int_1^n\frac{dx}{n+x}+s_n\\[5pt] &=\Bigl[\log(n+x)\Bigr]_1^n+s_n\\[5pt] &=\log\frac{2n}{n+1}+s_n\\[5pt] &=\log\frac2{1+\frac1n}+s_n \end{align*}\]
であり,$\underline{0<s_n<\dfrac1{n+1}}$ (下の注参照)により,
\[s_n\to0\ \ (n\to\infty)\]
であることに注意すると,
(求値) $\displaystyle=\lim_{n\to\infty}\left(\log\frac2{1+\frac1n}+s_n\right)=\underline{\boldsymbol{\log2}}$
注 斜線部分をすべて $y$ 軸に寄せてくると,縦 $\dfrac1{n+1}$,横 $1$ の長方形の中にすべて収まる.
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第3章 積分法
| スライド | ノート | |
| 1. 不定積分 | [無料] | |
| 2. 置換積分法(不定積分) | [無料] | |
| 3. 部分積分法(不定積分) | [無料] | |
| 4. 定積分とその性質 | [会員] | |
| 5. 置換積分法(定積分) | [会員] | |
| 6. 部分積分法(定積分) | [会員] | |
| 7. 定積分と微分法 | [会員] | |
| 8. 定積分と和の極限 | [会員] | |
| 9. 定積分と不等式 | [会員] | |
| 10. 定積分の応用(面積) | [会員] | |
| 11. 定積分の応用(体積) | [会員] | |
| 12. 定積分の応用(回転体の体積) | [会員] | |
| 13. 曲線の長さ |