7. 定積分と微分法【ノート】
1人で学べる！高校数学

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質
5. 置換積分法（定積分）
6. 部分積分法（定積分）
7. 定積分と微分法
8. 定積分と和の極限
9. 定積分と不等式
10. 定積分の応用（面積）
11. 定積分の応用（体積）
12. 定積分の応用（回転体の体積）
13. 曲線の長さ

7．定積分と微分法

7.1 定積分と微分法

$f(x)$ が連続関数，$a$ が定数のとき， $$\frac{d}{dx}{\int }_a^{x}f(t)dt=f(x)$$

証明

　$f(t)$ の不定積分を $F(t)$ とすると， $${\int }_a^{x}f(t)dt=F(x)-F(a)$$ 　よって， $$\frac{d}{dx}{\int }_a^{x}f(t)dt=F^{\prime }(x)-\{F(a){\}}^{\prime }=f(x)$$

■

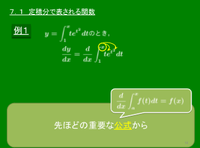
例1

　${\displaystyle y={\int }_1^{x}t{e}^{t^2}dt}$ のとき， $$\frac{dy}{dx}=\frac{d}{dx}{\int }_1^{x}t{e}^{t^2}dt=\underset{―}{x{e}^{x^2}}$$

例2

　${\displaystyle y={\int }_0^x(x-t)\cos tdt}$ のとき， $$\begin{array}{rl}& \text{×}\frac{dy}{dx}=(x-x)\cos x=0(??)\\ & \text{〇}y=x{\int }_0^x\cos tdt-{\int }_0^{x}t\cos tdt\\ & \therefore \frac{dy}{dx}=({\int }_0^x\cos tdt+x\cos x)-x\cos x\\ & =[\sin t{]}_0^x\\ & =\underset{―}{\sin x}\end{array}$$

補足

バリエーション 　$a$ を定数とする． $$\begin{array}{rl}& [1]\frac{d}{dx}{\int }_x^{a}f(t)dt=-f(x)\\ \\ & [2]\frac{d}{dx}{\int }_a^{g(x)}f(t)dt=f(g(x))g^{\prime }(x)\\ \\ & [3]\frac{d}{dx}{\int }_{h(x)}^{g(x)}f(t)dt=f(g(x))g^{\prime }(x)-f(h(x))h^{\prime }(x)\end{array}$$

例

　${\displaystyle y={\int }_{5x}^{x^2}\sin tdt}$ のとき， $$\begin{array}{rl}\frac{dy}{dx}& =(x^2{)}^{\prime }\times \sin x^2-(5x{)}^{\prime }\times \sin 5x\\ & =2x\sin x^2-5\sin 5x\end{array}$$

---

高校数学[総目次]

数学Ⅲ　第3章　積分法

	スライド	ノート	問題
1. 不定積分	[無料]
2. 置換積分法（不定積分）	[無料]
3. 部分積分法（不定積分）	[無料]
4. 定積分とその性質
5. 置換積分法（定積分）
6. 部分積分法（定積分）
7. 定積分と微分法
8. 定積分と和の極限
9. 定積分と不等式
10. 定積分の応用（面積）
11. 定積分の応用（体積）
12. 定積分の応用（回転体の体積）
13. 曲線の長さ