高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |

11.関数のグラフ
11.1 曲線の凹凸
微分可能な関数のグラフを考える.
ある区間で,接線の傾きが増加しているとき,グラフはその区間で下に凸という.逆にその区間で接線の傾きが減少しているとき,グラフはその区間で上に凸という.
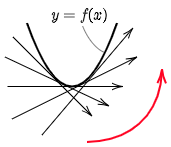
(接線の傾きが増加)
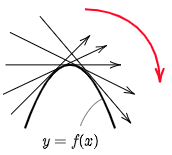
(接線の傾きが減少)
例えばある区間で,f′(x) の導関数である f′′(x) が常に正ならば,f′(x) は単調に増加するから,f(x) の接線の傾きは増加していく.即ち,その区間でグラフは下に凸である.ある区間で常に f′′(x)<0 となる場合も同様である.
まとめ 関数 f(x) が f′′(x) をもつとき,
常に f′′(x)>0 である区間でグラフは下に凸である.
常に f′′(x)<0 である区間でグラフは上に凸である.

11.2 変曲点
曲線の凹凸の境目を変曲点という.
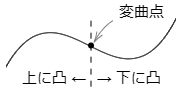
変曲点であるための必要条件
第2次導関数 f′′(x) をもつ関数 f(x) について,グラフが x=a を含むある区間において,x=a で上に凸から下に凸に変わるとする.
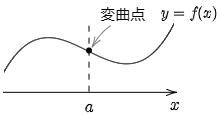
その区間内の x<a で f′′(x)<0,x>a で f′′(x)>0 だから,f′′(x) が連続ならば f′′(a)=0
x=a で下に凸から上に凸に変わる場合も,同様の理由で f′′(a)=0 となる.
定理 関数 f(x) の第2次導関数 f′′(x) が連続のとき, 点(a, f(a))が変曲点 ⟹ f′′(a)=0
注意
逆 (⇐) はいえない.
(反例)
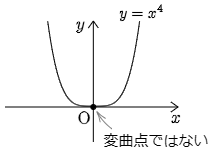
f(x)=x4 について,f′(x)=4x3,f′′(x)=12x2 であるから,f′′(0)=0.しかし,点(0,f(0)) は変曲点ではない.

11.3 漸近線の求め方
関数 y=f(x) のグラフにおいて,
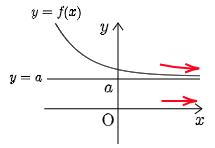
① limx→∞f(x)=a,またはlimx→−∞f(x)=a
→ 直線 y=a は漸近線.
② limx→a+0f(x)=∞,又はlimx→a+0f(x)=−∞
又はlimx→a−0f(x)=∞,又はlimx→a−0f(x)=−∞
→ 直線 x=a は漸近線.
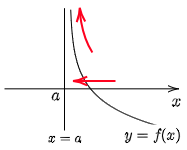
x→a+0 のケース
③ limx→∞{f(x)−(ax+b)}=0,又はlimx→−∞{f(x)−(ax+b)}=0
→ 直線 y=ax+b は漸近線.
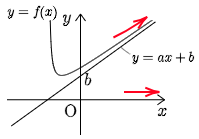
補足
③について,y=ax+b の a と b はどのようにしてわかるか?
もし,f(x) のグラフが x→∞ で直線 y=ax+b に漸近するならば,次が成り立つ:
a=limx→∞f(x)x, b=limx→∞{f(x)−ax}
証明
limx→∞{f(x)−(ax+b)}=0 ⋯① のとき, limx→∞f(x)−(ax+b)x=0 ∴limx→∞{f(x)x−a−bx}=0 ∴limx→∞{f(x)x−a}=0 (∵bx→0(x→∞)) ∴a=limx→∞f(x)x このようにして a が求まれば,①により, limx→∞{f(x)−ax}−b=0 ∴b=limx→∞{f(x)−ax}
■
補足
x→−∞ のとき直線 y=ax+b に漸近する場合も同様にして a と b を求めることができる.
注意
a=limx→∞f(x)x となる a が存在しても,漸近線が存在するとは限らない.例えば f(x)=x+√x のとき
f(x)x=1+1√x→1 (x→∞)
となるから a=1.然るに
limx→∞{f(x)−x}=limx→∞√x=∞
となるから,b=limx→∞{f(x)−ax} は有限確定値とならない.別の例として f(x)=sinx とすれば,はさみうちの原理により sinxx→0 (x→∞) だが,サインカーブに漸近線はない.
要するに x→∞ の場合では
曲線 y=f(x) が直線 y=ax+b を漸近線にもつ
⟺limx→∞{f(x)−(ax+b)}=0
⟺limx→∞{f(x)−ax}=b
⟹limx→∞f(x)x=a
※最後は矢印が右向きだけであることに注意
なのであって,limx→∞{f(x)−ax}=b (有限確定値) が成り立って初めて直線 y=ax+b が漸近線であるといえる訳である.
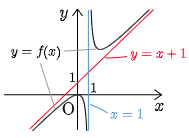
例題 f(x)=x2x−1 の漸近線を求めよ.
答
解答例を表示する
11.4 第2次導関数と極値
x=a を含むある区間で,f′′(x) が連続のとき,
[1] f′(a)=0 かつ f′′(a)<0 ならば,f(a) は極大値
[2] f′(a)=0 かつ f′′(a)>0 ならば,f(a) は極小値
証明
[1]の証明
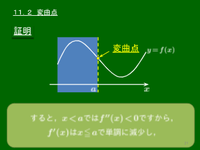
f′′(x) は連続だから,f′′(a)<0 ならば,x=a の十分近くでは常に f′′(x)<0 となる.
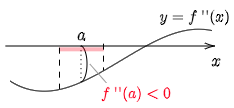
x=a の十分近くで f′′(a)<0
(赤い線分の範囲)
f′(x) の導関数 f′′(x) が常にf′′(x)<0 となるから,x=a の十分近くで f′(x) は単調に減少する.f′(a)=0 だから,f′(x) の符号は,x=a の前後で正から負に転じる.
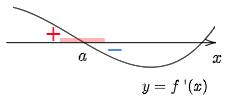
x=a の前後で正から負に転じる
即ち,f(a) は極大値である.
([2]も同様に証明される.)
■

このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |