高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |

10.関数の極大・極小
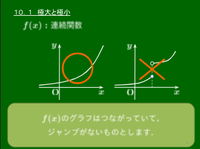
10.1 極大・極小
極大・極小については数学Ⅱ で既出である.極大や極小については数学Ⅱの方で詳細に説明したのでそちらを参照されたい.
極大値・極小値の定義
関数 f(x) は連続とする.
x=a を含む開区間で,どんな x(≠a) についても
f(a)>f(x) のとき,f(a) を f(x) の極大値
f(a)<f(x) のとき,f(a) を f(x) の極小値
という.また,極大値と極小値をあわせて極値という.
注意
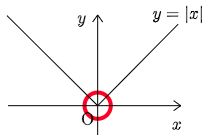
極大・極小は,微分可能性とは無関係である.例えば,関数f(x)=|x| は,x=0 で微分可能ではないが,x=0 で極小となっている.

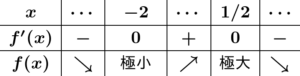
10.2 f(a) が極値であるための必要条件
微分可能な関数 f(x) が x=a で極値をとるとする.このとき f′(a)=0 が成り立つ.これは数学Ⅱの微分法のときにもお世話になっていたものである.f′(a)=0 は f(x) が x=a で極値をとるための必要条件である.
定理 f(x) が微分可能であるとき,
f(a) が極値 ⟹ f′(a)=0
発展的補足
f(x) が整式の場合などほとんど明らかと思われるこの定理.実際教科書にも証明が書かれていない.しかし例えば次の関数は x=0 で極小となるが,x=0 の付近で無限回振動するから,本当に f′(0)=0 なのかは明らかではない.(この関数については次節10.3に詳細な説明有.)
f(x)={x2(cos1x+2)(x≠0)0(x=0)
そこでこの定理を証明する.
証明
ある開区間で微分可能な関数 f(x) が,区間内の x=a で極大になるとすれば,区間内の任意の x について
f(x)≦f(a) ⋯ ①
が成り立つ.x=a で微分可能であるから
lim
となるが,①より左辺の分子は常に0以下であることに注意する.ここで x\to a+0 のとき,x-a\to +0 であるから
\lim_{x\to a+0}\frac{f(x)-f(a)}{x-a}\leqq 0\ \ \ \therefore f'(a)\leqq0
一方,x\to a-0 のとき,x-a\to -0 であるから
\lim_{x\to a-0}\frac{f(x)-f(a)}{x-a}\geqq 0\ \ \ \therefore f'(a)\geqq0
従って,f'(a)\leqq0 かつ f'(a)\geqq0 となるから, f'(a)=0.
x=a で極小となる場合も同様である.
■
注意
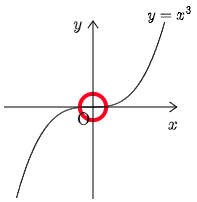
逆 (\Leftarrow) は成り立たない.
(反例) f(x)=x^3 のとき,f'(x)=3x^2 より f'(0)=0.しかるに f(0) は極値ではない.

10.3 f(a) が極値であるための十分条件
前節10.2では,「f(a) が極値である」というのが仮定で,「f'(a)=0」 というのが結論であった.今度は逆に,「f(a) が極値である」が結論にくるような命題を見てみよう.「 は f(a) が極値であるための十分条件である」の下線部に入るようなものである.
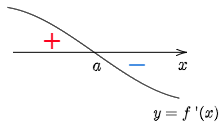
定理 x=a を含むある開区間で f(x) は微分可能かつ f'(a)=0 とする.この区間内において,
① x< a で f'(x) > 0,\ a < x で f'(x) < 0
\Longrightarrow f(a) は極大値
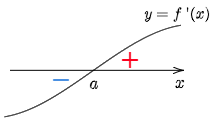
② x<a で f'(x) < 0,\ a < x で f'(x) > 0
\Longrightarrow f(a) は極小値
証明
① x<a で f'(x)>0 であるから,区間内の x\leqq a で f(x) は単調に増加する.従って区間内のすべての x\,(< a) で f(x)< f(a).
また,x>a で f'(x)<0 であるから,区間内の x\geqq a で f(x) は単調に減少する.従って区間内のすべての x\,(> a) で f(x)< f(a).
従って,この開区間において f(a) は最大値となるから極大値である.
② ①と同様に示される.
■
発展的注意
逆 (\Leftarrow) は成り立たない.
(反例)
f(x)=\left\{ \begin{array}{ll} x^2\left(\cos\dfrac1x+2\right)&(x\neq0\mbox{のとき})\\[5pt] 0&(x=0\mbox{のとき}) \end{array}\right.
この関数 f(x) は x\ne0 のとき,
\begin{align*} f'(x)&=2x\left(\cos\frac1x+2\right)+x^2\left\{-\sin\frac1x\cdot\left(-\dfrac1{x^2}\right)\right\}\\[5pt] &=2x\left(\cos\frac1x+2\right)+\sin\dfrac1x \end{align*}
であるから微分可能.また x=0 でも微分可能で,f'(0)=0.実際,
\begin{align*} \lim_{x\to0}\frac{f(x)-f(0)}{x-0}&=\lim_{x\to0}\dfrac{x^2\left(\cos\frac1x+2\right)}x\\[5pt] &=\lim_{x\to0}x\left(\cos\dfrac1x+2\right)\\[5pt] &=0\ \ (\because\mbox{はさみうちの原理}) \end{align*}
また,-1\leqq\cos\dfrac1x\leqq1 より 1\leqq\cos\dfrac1x+2\leqq3 であるから,f(x) のグラフは放物線 y=x^2 の上側かつ y=3x^2 の下側となり,f(0)=0 と定義されていることから f(0) は極小値である.
ところが,f(x) は x=0 の近くで x^2 と 3x^2 の間を無限回振動するから,f'(x) の符号は x < 0 及び x > 0 それぞれで定符号ではない.
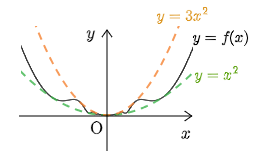
原点の近くで無限回振動する.

10.4 \dfrac{f(x)}{g(x)} の極値
微分可能な関数 \dfrac{f(x)}{g(x)} が,x=a で極値をとるならば, \frac{f(a)}{g(a)}=\frac{f'(a)}{g'(a)}\ \ \ \ (\mbox{ただし},g'(a)\neq 0)
証明
h(x)=\dfrac{f(x)}{g(x)} とおくと, h'(a)=\frac{f'(a)g(a)-f(a)g'(a)}{\{g(a)\}^2}=0 であるから, \frac{f(a)}{g(a)}=\frac{f'(a)}{g'(a)}
■
例題 f(x)=\dfrac{4x+3}{x^2+1} の極値を求めよ.
こたえ
解答例を表示する
このページで疑問は解決されましたか?
こちら から数学に関するご質問・ご要望をお寄せください。
高校数学[総目次]
数学Ⅲ 第2章 微分法
| スライド | ノート | 問題 | |
| 1. 微分係数と導関数 | [無料] | ||
| 2. 合成関数の導関数 | [無料] | ||
| 3. 逆関数の微分法 | [無料] | [会員] | |
| 4. 三角関数の導関数 | [会員] | ||
| 5. 対数関数・指数関数の導関数 | [会員] | ||
| 6. 媒介変数表示と導関数 | [会員] | ||
| 7. 陰関数の導関数 | [会員] | ||
| 8. 平均値の定理 | [会員] | ||
| 9. 関数の値の変化 | [会員] | [会員] | |
| 10. 関数の極大・極小 | [会員] | ||
| 11. 関数のグラフ | [会員] |